Partial Differential Equations
Linear algebra is the mathematical guide of choice for implementing the
principle of unit-economy61
applied to partial differential equations. The present chapter considers two
kinds:
- Single linear partial differential equations corresponding to the linear
system
However, instead of merely exhibiting general solutions to such a system, we
shall take seriously the dictum which says that a differential equation
is never solved until ``boundary'' conditions have been imposed on its
solution. As identified in the ensuing section, these conditions are not
arbitrary. Instead, they fall into three archetypical classes determined by
the nature of the physical system which the partial differential equation
conceptualizes.
- Systems of pde's corresponding to an over-determined system
 |
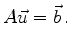(61) |
The idea for solving it takes advantage of the fundamental subspaces62of
[#!StrangLinearAlgebra!#]. Let
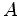be a
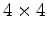matrix having rank
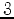. Such a matrix, we recall, has a vector
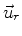which satisfies 
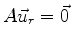, or, to be more precise
 |
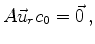(62) |
where
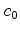is any non-zero scalar. Thus
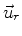spans
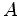's one-dimensional nullspace
This expresses the fact that the columnes of
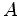are linearly dependent.
In addition we recall that the four rows of
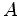are linearly dependent also, a fact which is expressed by the existence of a
vector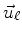 
which satisfies
 |
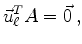(63) |
and which therefore spans
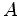's one-dimensional left nullspace
In general there does not exist a solution to the over-determined system Eq.(6.1).
However, a solution obviously does exist if and only if
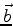satisfies
Under such a circumstance there are infinitely many solutions, each one
differing from any other merely by a multiple of the null vector
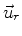. The most direct path towards these solutions is via eigenvectors.
One of them is, of course, the vector
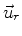in Eq.(6.2). The other three,
which (for the
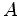under consideration) are linearly independent, satisfy
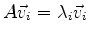with
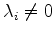, or, in the interest of greater precision (which is needed in Section
6.2.3),
where, like
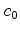, the
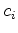's are any non-zero scalars. Because of the simplicity of
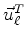for the
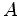under consideration one can find the eigenvectors
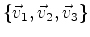, and hence their eigenvalues, by a process of inspection. These vectors span
the range of
,
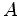and therefore determine those vectors
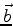for which there exists a solution to Eq.(6.1).
Such vectors belong to
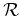and thus have the form
These eigenvectors also serve to represent the corresponding solution,
This, the fact that
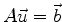, and the linear independence of the
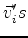imply that the scalars
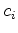satisfy the three equations
As expected, the contribution
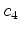along the direction of the nullspace element is left indeterminate. These ideas
from linear algebra and their application to solving a system, such as Eq.(6.1),
can be extended to corresponding systems of partial differential equations. The
Maxwell field equations, which we shall analalyze using linear algebra, is a
premier example. In this extension the scalar entries of
and
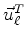get replaced by differential operators, the vectors
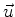and
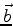by vector fields, the scalars
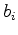and
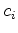by scalar fields, the eigenvalues
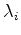by a second order wave operator, and the three Eqs.(6.7)-
by three inhomogeneous scalar wave equations corresponding to what in physics
and engineering are called
- transverse electric (
),
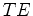- transverse magnetic (
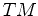), and
- transverse electric magnetic (
),
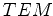modes respectively.
|
