| Fluids Mechanics and Fluid Properties |
Fluids Mechanics and Fluid Properties
What is fluid mechanics? As its name suggests it is the branch of applied
mechanics concerned with the statics and dynamics of fluids - both liquids and
gases. The analysis of the behaviour of fluids is based on the fundamental laws
of mechanics which relate continuity of mass and energy with force and momentum
together with the familiar solid mechanics properties.
Objectives of this section
- Define the nature of a fluid.
- Show where fluid mechanics concepts are common with those of solid
mechanics and indicate some fundamental areas of difference.
- Introduce viscosity and show what are Newtonian and non-Newtonian
fluids
- Define the appropriate physical properties and show how these allow
differentiation between solids and fluids as well as between liquids and
gases.
Fluids
There are two aspects of fluid mechanics which make it different to solid
mechanics:
- The nature of a fluid is much different to that of a solid
- In fluids we usually deal with continuous streams of fluid
without a beginning or end. In solids we only consider individual
elements.
We normally recognise three states of matter: solid; liquid and gas.
However, liquid and gas are both fluids: in contrast to solids they lack the
ability to resist deformation. Because a fluid cannot resist the deformation
force, it moves, it flows under the action of the force. Its shape
will change continuously as long as the force is applied. A solid can resist
a deformation force while at rest, this force may cause some displacement
but the solid does not continue to move indefinitely.
The deformation is caused by shearing forces which act
tangentially to a surface. Referring to the figure below, we see the force F
acting tangentially on a rectangular (solid lined) element ABDC. This is a
shearing force and produces the (dashed lined) rhombus element A'B'DC.
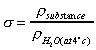
Shearing force, F, acting on a fluid element.
We can then say:
A Fluid is a substance which deforms continuously,
or flows, when subjected to shearing forces.
and conversely this definition implies the very important point that:
If a fluid is at rest there are no shearing forces acting.
All forces must be perpendicular to the planes which the are acting.
When a fluid is in motion shear stresses are developed if the particles
of the fluid move relative to one another. When this happens adjacent
particles have different velocities. If fluid velocity is the same at every
point then there is no shear stress produced: the particles have zero
relative velocity.
Consider the flow in a pipe in which water is flowing. At the pipe wall
the velocity of the water will be zero. The velocity will increase as we
move toward the centre of the pipe. This change in velocity across the
direction of flow is known as velocity profile and shown graphically in the
figure below:
Velocity profile in a pipe.
Because particles of fluid next to each other are moving with different
velocities there are shear forces in the moving fluid i.e. shear
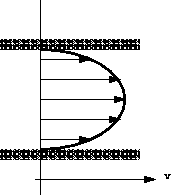
forces are normally present in a moving fluid. On the other hand, if
a fluid is a long way from the boundary and all the particles are travelling
with the same velocity, the velocity profile would look something like this:
Velocity profile in uniform flow
and there will be no shear forces present as all particles have zero
relative velocity. In practice we are concerned with flow past solid
boundaries; aeroplanes, cars, pipe walls, river channels etc. and shear
forces will be present.
Newton's Law of Viscosity
How can we make use of these observations? We can start by considering a
3d rectangular element of fluid, like that in the figure below.
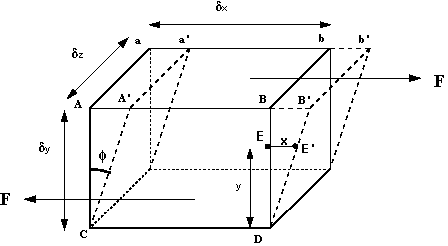
Fluid element under a shear force
The shearing force F acts on the area on the top of the element. This
area is given by
 .
We can thus calculate the shear stress which is equal to force per
unit area i.e.
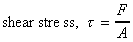
The deformation which this shear stress causes is measured by the size of
the angle f
and is know as shear strain.
In a solid shear strain, f
, is constant
for a fixed shear stress t
.
In a fluid f
increases for as long as
t
is applied - the fluid flows.
It has been found experimentally that the rate of shear stress
(shear stress per unit time, t
/time) is directly
proportional to the shear stress.
If the particle at point E (in the above figure) moves under the shear
stress to point E' and it takes time t to get there, it has moved the
distance x. For small deformations we can write
shear strain
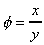
where
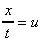is the velocity of the particle at E.
Using the experimental result that shear stress is proportional to rate
of shear strain then
The term
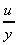is the change in velocity with y, or the velocity gradient, and may be
written in the differential form
 .
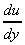The constant of proportionality is known as the dynamic viscosity,
 ,
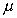of the fluid, giving
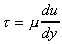
This is known as Newton's law of viscosity.
Fluids vs. Solids
In the above we have discussed the differences between the behaviour of
solids and fluids under an applied force. Summarising, we have;
- For a solid the strain is a function of the applied stress
(providing that the elastic limit has not been reached). For a fluid,
the rate of strain is proportional to the applied stress.
- The strain in a solid is independent of the time over which
the force is applied and (if the elastic limit is not reached) the
deformation disappears when the force is removed. A fluid
continues to flow for as long as the force is applied and will not
recover its original form when the force is removed.
It is usually quite simple to classify substances as either solid or
liquid. Some substances, however, (e.g. pitch or glass) appear solid under
their own weight. Pitch will, although appearing solid at room temperature,
deform and spread out over days - rather than the fraction of a second it
would take water.
As you will have seen when looking at properties of solids, when the
elastic limit is reached they seem to flow. They become plastic. They still
do not meet the definition of true fluids as they will only flow
after a certain minimum shear stress is attained.
Newtonian /
Non-Newtonian Fluids
Even among fluids which are accepted as fluids there can be wide
differences in behaviour under stress. Fluids obeying Newton's law where the
value of m
is constant are known as Newtonian
fluids. If m
is constant the shear stress is
linearly dependent on velocity gradient. This is true for most common
fluids.
Fluids in which the value of m
is not constant
are known as non-Newtonian fluids. There are several categories of
these, and they are outlined briefly below.
These categories are based on the relationship between shear stress and
the velocity gradient (rate of shear strain) in the fluid. These
relationships can be seen in the graph below for several categories
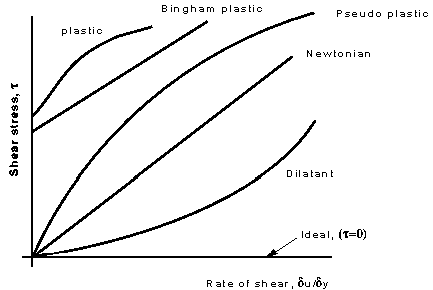
Shear stress vs. Rate of shear strain d
u/d
y
Each of these lines can be represented by the equation
where A, B and n are constants. For Newtonian fluids A = 0, B =
m
and n = 1.
Below are brief description of the physical properties of the several
categories:
- Plastic: Shear stress must reach a certain minimum before
flow commences.
- Bingham plastic: As with the plastic above a minimum shear
stress must be achieved. With this classification n = 1. An example is
sewage sludge.
- Pseudo-plastic: No minimum shear stress necessary and the
viscosity decreases with rate of shear, e.g. colloidial substances like
clay, milk and cement.
- Dilatant substances; Viscosity increases with rate of shear
e.g. quicksand.
- Thixotropic substances: Viscosity decreases with length of
time shear force is applied e.g. thixotropic jelly paints.
- Rheopectic substances: Viscosity increases with length of
time shear force is applied
- Viscoelastic materials: Similar to Newtonian but if there is
a sudden large change in shear they behave like plastic.
There is also one more - which is not real, it does not exist - known as
the ideal fluid. This is a fluid which is assumed to have no
viscosity. This is a useful concept when theoretical solutions are being
considered - it does help achieve some practically useful solutions.
- Liquids vs. Gasses
Although liquids and gasses behave in much the same way and share many
similar characteristics, they also possess distinct characteristics of their
own. Specifically
- A liquid is difficult to compress and often regarded as being
incompressible.
A gas is easily to compress and usually treated as such - it changes
volume with pressure.
- A given mass of liquid occupies a given volume and will occupy the
container it is in and form a free surface (if the container is of a
larger volume).
A gas has no fixed volume, it changes volume to expand to fill the
containing vessel. It will completely fill the vessel so no free surface
is formed.
Causes of Viscosity in Fluids
Viscosity in Gasses
The molecules of gasses are only weakly kept in position by molecular
cohesion (as they are so far apart). As adjacent layers move by each
other there is a continuous exchange of molecules. Molecules of a slower
layer move to faster layers causing a drag, while molecules moving the
other way exert an acceleration force. Mathematical considerations of
this momentum exchange can lead to Newton law of viscosity.
If temperature of a gas increases the momentum exchange between
layers will increase thus increasing viscosity.
Viscosity will also change with pressure - but under normal
conditions this change is negligible in gasses.
Viscosity in Liquids
There is some molecular interchange between adjacent layers in
liquids - but as the molecules are so much closer than in gasses the
cohesive forces hold the molecules in place much more rigidly. This
cohesion plays an important roll in the viscosity of liquids.
Increasing the temperature of a fluid reduces the cohesive forces and
increases the molecular interchange. Reducing cohesive forces reduces
shear stress, while increasing molecular interchange increases shear
stress. Because of this complex interrelation the effect of temperature
on viscosity has something of the form:
where
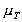is the viscosity at temperature TC, and
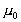is the viscosity at temperature 0C. A and B are constants for a
particular fluid.
High pressure can also change the viscosity of a liquid. As pressure
increases the relative movement of molecules requires more energy hence
viscosity increases.
|
