Operational amplifiers can be used to perform mathematical operations on voltage signals such as inversion, addition, subtraction, integration, differentiation, and multiplication by a constant.  You need to understand how to figure out what an operational amplifier circuit does.  We will start with a simple circuit so that we can examine a method that will permit you to figure out how these circuits work and then you will have a more general method you can use for more complex circuits.  So, you have two goals in this section.

   Given an inverting amplifier op-amp circuit with resistor values,

    Be able to compute the gain of the circuit.

   Given an operational amplifier op-amp circuit similar to the inverting amplifier,

Be able to compute the output voltage of the circuit in terms of the signals and electrical elements in the circuit.

Analyzing the Inverting Amplifier

        The circuit we will examine is shown below.  This circuit amplifies a voltage by a factor (- R_o / R₁).  What is important in this circuit is that it amplifies by almost  exactly (-R_o /R₁) so that the gain of the circuit can be controlled precisely by controlling the resistor values precisely.  The gain of the circuit will not depend upon paramters of the "Op-Amp".  We'll analyze this circuit to get a mathematical prediction of how it works.

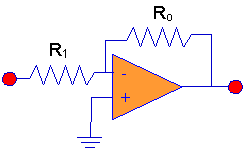
Note:  The power supply connections are not shown.  For the operational amplifier to function properly you will need to supply power to it.  Also, note that the input labelled "+" is referred to as the non-inverting input, and the input labelled "-" is referred to as the inverting input.  The operational amplifier amplifies the difference between the non-inverting input and the inverting input.  In other words, the output of the operational amplifier is:

• Op-amp output voltage = A (V₊ - V_-) where

• A is the gain - usually a pretty large number, often greater than 100,000 or 200,000.

• V₊  is the voltage at the non-inverting input (measured to ground).

• V_- is the voltage at the inverting input (measured to ground).

Because the operational amplifier amplifies the difference between the two voltages - rather than a single voltage - the operational amplifier is a differential amplifier.

        The operational amplifier has a long history.  It first appeared in vacuum tube manifestations in the 1950s.  These amplifiers were heavy, expensive and prone to failure.  They usually required a power supply that most normal people could not lift.  The amplifiers cost about a hundred dollars, and the supplies several hundred in an era when a hundred dollars was worth much more than today's value.  In the 1960s transistorized versions of operational amplifiers came on the market, and in the middle to late 1960s the first integrated circuit operational amplifiers came on the market.  (Although different technologies were used at different times, the amplifiers had characteristics in common that marked them as operational amplifiers even though built in widely different forms!)

        In this era of team engineering it is interesting to note that one individual, Robert Widlar, was responsible for the development of the integrated circuit operational amplifier in a form that led to wide acceptance.  Today, thanks to Widlar and many others operational amplifiers are available for less than 25 cents and the operational amplifier is probably the most widely used analog integrated circuit.

        Widlar is known not just for his creativity, but also for his zany antics.  Of course, those two characteristics might just go together.  When National Semiconductor went into a period of austerity, and stopped mowing the grass, Bob Widlar brought a sheep and turned it loose to graze.

Analysis Of The Inverting Amplifier

        To analyze the inverting amplifier, we start by making an assumption that the output voltage, V_out, is some "reasonable" value - a value somewhere between the values of the positive and negative power supply voltages.  That may well seem like an odd place to start, but we can begin to look at the consequences of making that assumption.

        For example, we might have an output voltage of ten (10) volts. We can figure out what input voltage caused that output voltage of ten volts.  If the gain of the operational amplifier is 100,000, then the input difference, (V+ - V-), must be 10/100,000 or .00001 volts.  That's 100 microvolts, and it's pretty darn small.

        Notice what happens here.  This assumption that the difference between the inverting and noninverting input voltages is just a consequence of the very high gain of the operational amplifier.  It's not special to this circuit.  It's a general idea that we can make use of in other amplifier circuits.

        For all practical purposes that voltage is close enough to zero that we will call it zero when we calculate how the circuit behaves.  We know it isn't zero, but it has such a small value that it will not affect any of our calculations.  You'll need to remember the logic here.

• If the output of the operational amplifier is some reasonable value (usually ten volts or less, either positive or negative, as long as the amplifier isn't saturated.  Then all bets are off.),

• And, if the operational amplifier has a really high gain (and remember 100,000 is probably a low value of the gain for typical amplifiers),

• Then, the voltage at the input of the amplifier is zero for all practical purposes.

        And, note the following:

• For the voltage to be zero the gain of the amplifier would have to be infinite.  When people discuss this assumption, they often refer to it as the infinite gain assumption.

• What the infinite gain assumption reduces to is that we can consider the voltage difference between the two inputs to be zero.

        For all practical purposes that voltage is close enough to zero that we will call it zero when we calculate how the circuit behaves.  We know it isn't zero, but it has such a small value that it will not affect any of our calculations.

        Since the difference between the operational amplifier input voltages are practially zero and the internal input resistance is very large, we can  make the assumption that the current flowing into the amplifier through either of the input terminals is so small as to be negligible.  Most of the time that's a good assumption because:

• The input voltage is small (See above.).

• The input resistance of the op-amp is large.

Here is a modified circuit diagram that shows the input resistance of the operational amplifier.  You can visualize the input resistance as a resistor connected between the input terminals of the operational amplifier.

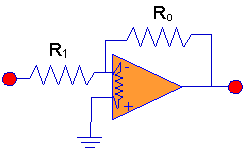
        Let's take a minute to summarize the few assumptions we have made so far.

• The output voltage, V_out, is within the value between the positive and negative voltage supply.  It's a "reasonable" value.

• The input difference, (V₊ - V_- ) is small enough that we can consider the value to be approximately zero.  This is due to large gain of the amplifier - the infinite gain assumption.  We will assume that the input voltage difference is zero.

• Since we will treat the input difference as zero, and assume input resistance (the resistance between the non-inverting and inverting inputs) is infinte, then the current flowing through both of the inputs of the amplifier will also be so small that it is negligible.  We will assume that no current enters the input terminals of the op-amp.

        Assuming that the input difference is small, we can write KCL at the inverting node:  (Notice the little red dot at the inverting node in the circuit diagram.)  (Note also, that we have defined two voltages, V₁ and V_out that are both measured with respect to the ground.)

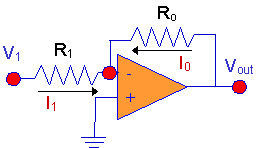
        Here's the KCL equation using the assumption that the voltage at the amplifier input - at the input node - is zero.

Technically, we can write KCL in terms of all the voltages involved (taking V₊ and V_- as the voltages - with respect to ground - at the "+" and "-" terminals respectively).  Doing that we obtain:

        However, since we assume that there is no voltage difference between V₊ and V_- , we can replace V_- with V₊ and we have the inverting input terminal connected to ground, so V_- = 0.  That means we get: