Operational amplifiers are useful devices that can be used for numerous types of
operations on signals. In this lesson you will examine a number of
operational amplifier circuits that are useful in many situations. To
predict the behavior of remember these facts about how operational amplifiers
perform when they operate out of saturation.
-
The input difference, (V+
- V- ) is small enough that we can consider the value to be
approximately zero. This is due to large gain of the amplifier - the
infinite gain assumption. We assume that the
input voltage difference is zero.
-
Since we will treat the input
difference as zero, and assume input resistance (the resistance between the
non-inverting and inverting inputs) is infinte, then the current flowing through
both of the inputs of the amplifier will also be so small that it is negligible.
We assume that no current enters the input terminals of the op-amp.
As we encounter different circuits we will use these
assumptions to predict circuit behavior.
The Unity Gain Buffer Amplifier
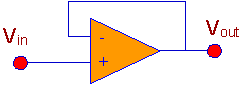
If the difference between V+ and V- is negligibly small so
that V+ = V- we must have:
This
circuit is often used when a voltage source with a high internal impedance is
used, and you want to draw more current than the source can deliver. The
solution is to use this circuit to make a copy of the original voltage, Vin,
and that copy, Vout, appears at the output of an operational
amplifier that can often deliver more current without lowering the output
voltage because the internal resistance of the operational amplifier is lower
than the internal resistance of the original source.
The Summing Amplifier
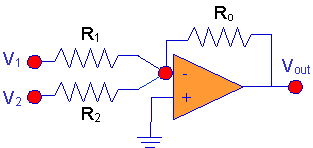
Here's
what happens in sequence.
-
The first assumption leads us
to assume that V- = 0. In other words, the voltage at
the inverting input becomes a virtual ground.
In practice, that point is at ground potential - zero volts.
-
We write KCL at the node
at the inverting input - the virtual ground point. The KCL equation is
relatively simple.
-
(V1
- V- )/R1 + (V2 - V-
)/R2 + (Vout - V- )/R0
= 0
-
Since V- is assumed
to be zero, we get:
-
V1 / R1
+ V2 / R2 + Vout
/ R0 = 0
-
or
-
Vout
/ R0 = - V1 / R1 - V2
/ R2
-
or
-
Vout
= - (V1 / R1 + V2
/ R2 )R0
-
or
-
Vout = - (V1R0
/ R1 + V2R0
/ R2 )
The result is that the output is a weighted sum of
the two inputs. If we just wanted to add the two inputs we could choose
all of gthe resistors to be equal. Of course, we get a minus sign, but
that's unavoidable.
Q1
If you want to get rid of the minus sign, do you have any options?
Where
would you use a circuit like this?
-
If you have two microphones and
you want to add the signals to produce one signal that is the sum of the two -
so you can hear both signals together - you can use this circuit. In audio
circles, that's called a mixer.
-
In a common type of control
system, signals proportional to an error signal, and the integral of the error
are added together, and this circuit is often used. That's a
PI (Proportional + Integral) controller.
We're sure that you can - and will - find many other
uses for the summing amplifier.
The Integrator
The
integrator does just what the name implies. It integrates - in the
calculus sense - the input signal to produce the output signal. There is a
scaling factor and a minus sign again, but that's pretty much what happens.
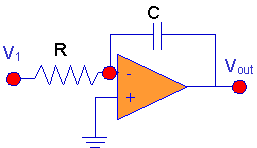
Here's the analysis. We make the usual
assumptions:
Then, we have - after we write KCL:
-
C(dVout/dt) +
V1/R = 0
-
Then:
A Circuit with Infinite Input Resistance/Impedance and a Gain Larger Than 1.0
This circuit is particularly useful when you need to avoid loading the signal
circuit, and you also want a gain larger than 1, and you don't want to have to
build one of those pesky inverter circuits.
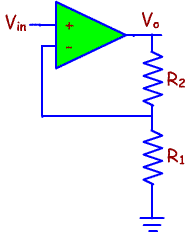
In this circuit, the two
resistors form a voltage divider.
|

