Resistor Combinations

Combinations of Resistors

Resistors do not occur in isolation. They are almost always part of a larger circuit, and frequently that larger circuit contains many resistors. It is often the case that resistors occur in combinations that repeat.

Goals

What are our goals for this lesson? Here are some.

Given a circuit with a number of resistors,

Be able to determine resistor combinations within the circuit where two or more resistors can be combined.

Be able to replace series and parallel resistor combinations with the correct equivalent resistors.

Combinations of Resistors

In this lesson we will look at two recurring resistor combinations, series combinations and parallel combinations. Those are common combinations, not only for resistors but other elements as well. (For example, we can speak of "a resistor in series with a capacitor".)

We'll start by examining series and parallel combinations and then move on to identifying those combinations when they are "buried" within a larger circuit. What we're doing is learning how to recognize small portions of larger circuits. Experts do that.

Series Combinations of Resistors

Two elements are said to be in series whenever the same current physically flows through both of the elements. The critical point is that the same current flows through both resistors when two are in series. The particular configuration does not matter. The only thing that matters is that exactly the same current flows through both resistors. Current flows into one element, through the element, out of the element into the other element, through the second element and out of the second element. 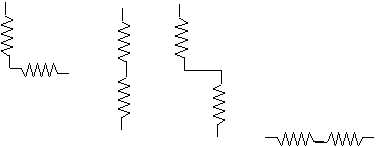No part of the current that flows through one resistor "escapes" and none is added. This figure shows several different ways that two resistors in series might appear as part of a larger circuit diagram.

Questions

Here is a circuit you may have seen before. Answer the questions below for this circuit.

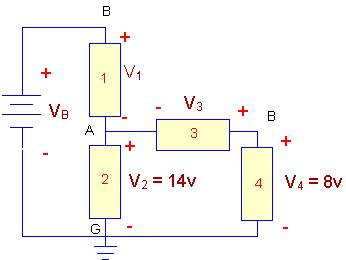
Q1. Are elements #3 and #4 in series?

Q2. Are elements #1 and #2 in series?

Q3. Is the battery in series with any element?

You might wonder just how often you actually find resistors in series. The answer is that you find resistors in series all the time.

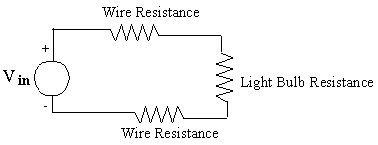
An example of series resistors is in house wiring. The leads from the service entrance enter a distribution box, and then wires are strung throughout the house. The current flows out of the distribution box, through one of the wires, then perhaps through a light bulb, back through the other wire. We might model that situation with the circuit diagram shown below.

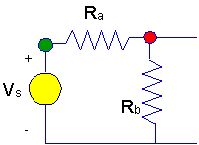
In many electronic circuits series resistors are used to get a different voltage across one of the resistors. We'll look at those circuits, called voltage dividers, in a short while. Here's the circuit diagram for a voltage divider.

Besides resistors in series, we can also have other elements in series - capacitors, inductors, diodes. These elements can be in series with other elements. For example, the simplest form of filter, for filtering low frequency noise out of a signal, can be built just by putting a resistor in series with a capacitor, and taking the output as the capacitor voltage.

As we go along you'll have lots of opportunity to use and to expand what you learn about series combinations as you study resistors in series.

Let's look at the model again. We see that the wires are actually small resistors (small value of resistance, not necessarily physically small) in series with the light bulb, which is also a resistor. We have three resistors in series although two of the resistors are small. We know that the resistors are in series because all of the current that flows out of the distribution box through the first wire also flows through the light bulb and back through the second wire, thus meeting our condition for a series connection. Trace that out in the circuit diagram and the pictorial representation above.

Let us consider the simplest case of a series resistor connection, the case of just two resistors in series. We can perform a thought experiment on these two resistors. Here is the circuit diagram for the situation we're interested in.

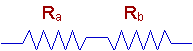
Imagine that they are embedded in an opaque piece of plastic, so that we only have access to the two nodes at the ends of the series connection, and the middle node is inaccessible. If we measured the resistance of the combination, what would we find? To answer that question we need to define voltage and current variables for the resistors. If we take advantage of the fact that the current through them is the same (Apply KCL at the interior node if you are unconvinced!) then we have the situation below.

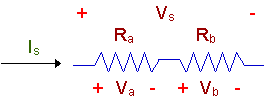
Note that we have defined a voltage across each resistor (V_a and V_b) and current that flows through both resistors (I_s) and a voltage variable, V_s, for the voltage that appears across the series combination.

Let's list what we know.

• The current through the two resistors is the same.

• The voltage across the series combination is given by:

• V_s= V_a + V_b

• The voltages across the two resistors are given by Ohm's Law:

• V_a = I_s R_a

• V_b = I_s R_b

We can combine all of these relations, and when we do that we find the following.

• V_s= V_a + V_b

• V_s= I_s R_a + I_s R_b

• V_s= I_s (R_a + R_b)

• V_s= I_s R_series

Here, we take R_series to be the series equivalent of the two resistors in series, and the expression for R_series is:

What do we mean by series equivalent? Here are some points to observe.

• If current and voltage are proportional, then the device is a resistor.

• We have shown thatV_s= I_s R_series, so that voltage is proportional to current, and the constant of proportionality is a resistance.

• We will call that the equivalent series resistance.