Temperature sensors are often sensing devices embedded within some sort of insulation.  The insulation may often be for electrical purposes - to isolate the sensor electrically.  However, good electrical insulation is often also good thermal insulation, and the presence of that insulation causes the sensor to respond tardily when the sensor heats up.

        We'll try to put together a simple model to help explain that behavior.  When we say explain, we mean to imply that we are looking for a mathematical model for a mathematical explanation.  We start with a physical model - the one shown below.

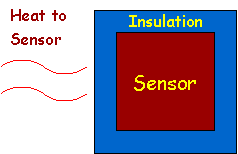
In this model, we assume the following.

• The sensor is embedded within a layer of insulation that insulates the sensor from the heat source that the sensor is supposed to experience.

• We assume that the temperature of the sensor is T_s(t) - and it is going to be a function of time because we want to see how it changes in time when the applied temperature changes.

• We represent the external temperature with T_a(t).

• We assume that the heat flow into the sensor from the outside is given by:

• Heat Flow To Sensor = [T_a(t). - T_s(t)]/R_th

• In other words, the heat flow to the sensor depends upon the difference between the external temperature and the sensor temperature, and the heat flow gets less as the thermal resistance between the sensor and the external temperature becomes higher (better insulation).

• We assume that a given amount of heat raises the temperature of the sensor by an amount proportional to the amount of heat.  In other words, the temperature of the sensor is proportional to the amount of heat energy it contains.

• Heat Content Of Sensor = C_sT_s(t).

• Then, we can write an equation that relates the heat content of the sensor to the flow of heat into the sensor.  Unfortunately, this is going to be a differential equation.

• Rate of Change of Heat Content of Sensor = Rate of Heat Flow to Sensor

• C_sdT(t)_s/dt = [T_a(t). - T_s(t)]/R_th

• In this situation, a little re-definition of variables will produce a differential equation that is a lot easier to solve.

• Define: DT(t) =  [T_a(t). - T_s(t)]

• If the surrounding temperature, T_a(t), is constant, then dDT(t)/dt = - dT_s(t)/dt, and

• dDT(t)/dt  = - dT_s(t)/dt = -[T_a(t). - T_s(t)]/R_thC_s = DT(t)/t_th

  , and this can be rewritten as:

• dDT(t)/dt = -DT(t)/R_thC_s = -DT(t)/t_th

• t_th= Thermal Time Constant

• You can check that it actually has the units of time.

• Now, our goal is to take this differential equation description and use it to get a meaningful description of how the sensor responds.

        There are a few special situations that we will examine here.  That won't get us to a general description that would allow us to predict what would happen in every situation, but that's what the differential equation is for.  Here we will solve the differential equation for a few special cases in order to get an appreciation of what the time behavior of the sensor is.  The situations we will examine are:

• The case where the temperature of the surroundings changes suddenly and has to come to equilibrium at the new temperature.

• The case where the sensor is taken from a temperature then put into new surroundings and allowed to cool (or rise?) to the temperature of the surroundings.

However, it does not matter which of those situations we have.  In either case, the differential equation and the solution to the differential equation is the same.  We will find that the only thing that matters is the initial temperature of the sensor, and the final temperature it achieves - the temperature of its' surroundings.

        Imagine that the sensor is taken from a temperature and has to come to equilibrium with new surroundings.  Imagine a situation where the sensor is at a high temperature and is removed to a cooler temperature.  The differential equation we derived above still holds, and we can solve it here.  Let's look at that differential equation again.

• dDT(t)/dt = -DT(t)/R_thC_s = -DT(t)/t_th

• But, initially, DT(0) =  [T_a(0). - T_s(0)], and this quantity is fixed when you start the experiment.

• We can solve the differential equation above to get:

• DT(t) = DT(0)e^-t/tth

This time function will look like the following plot.

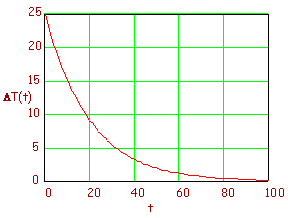
This plot is done for the following parameters:

• DT(0) = 25 degrees
• t_th= 20 seconds

Points to note on this plot include the following.

• The temperature difference, DT(t), asymptotically goes to zero as time gets large.

• Since the time constant for the example was 20 seconds, it seems as though it takes about five (5) time constants (100 seconds on the plot) for the response to decay to the point where you can safely say that it has reached steady state - even though that steady state is only approached and never reached theoretically.

        If we have a situation there the sensor finds itself in a surrounding temperature higher than its' current temperature, then the sensor temperature will have to rise.  In that situation, we have a plot like the one below.

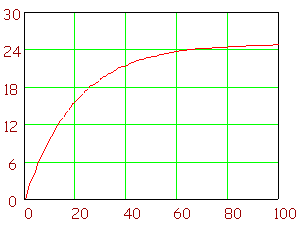
This plot is done for the same parameters as above, except that the actual temperature is plotted here.  If you get a plot like this - in lab, for example - you will need to extract the temperature difference.  Here the steady state looks to be 25 - starting from 0 - and the temperature difference - that decays to zero - is obtained by subtracting the actual temperature from 25 degrees.