| Sensors Dynamics |
Sensors
Sensors
are devices that are used to measure physical variables like temperature, pH,
velocity, rotational rate, flow rate, pressure and many others. Today,
most sensors do not indicate a reading on an analog scale (like a thermometer),
but, rather, they produce a voltage or a digital signal that is indicative of
the physical variable they measure. Those signals are often imported into
computer programs, stored in files, plotted on computers and analyzed to death.
Sensors come in many kinds and shapes to measure all kinds of physical
variables. However, many sensors have some sort of voltage output.
There are a number of implications to that. Here are some.
-
If a sensor has a voltage
output, then it is a voltage source
that is controlled by the physical variable it measures.
-
If the sensor is a voltage
source, you need to remember that no physical voltage sources are
ideal, and non-ideal voltage sources are usually best described with a
Thevinin Equivalent Circuit that contains the voltage source and an internal
resistance.
-
If a source has an internal
resistance, there is a possibility of loading the source. If a significant
load is attached to the source, the terminal voltage will drop. At that
point, the terminal voltage is not what you expect it to be (from calibrations,
spec sheets, etc.)
Example
The LM35 spec sheet lists an internal resistance of 0.1W .
Since the LM35 produces .01v/oC, you can compute how much
current you can draw for a specified change in reading.
Say you are measuring 50oC. Then the output voltage
should be 0.5v. To change that output voltage to 0.49v - and error of one
degree - you would have to have a voltage drop of .01v across the internal
resistance of 0.1W .
would take .1A or 100mA. That would be a lot of current to draw from the
LM35 and is beyond the limit of what it can supply.
A More Advanced Model - Using System Dynamics
Often sensors have time constants. (You can refer, for example, to the
charts in the
LM35 spec sheet.) If you take the sensor
time constant into account, you would not expect the output voltage to change
immediately when the temperature changed suddenly. A circuit/system model
that takes that into account is shown below.
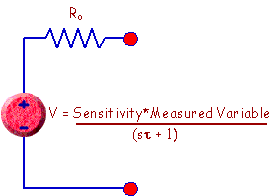
If you are knowledgeable
about Laplace transforms, the denominator quantity indicates that the input
(Measured Variable) is processed by a system with a single time constant (one
pole). If you use this sensor in a block diagram, you should take that
transfer function into account.
|