Temperature
Sensor - The Thermistor
Thermistors are inexpensive, easily-obtainable temperature sensors. They
are easy to use and adaptable. Circuits with thermistors can have
reasonable outout voltages - not the millivolt outputs thermocouples have.
Because of these qualities, thermistors are widely used for simple temperature
measurements. They're not used for high temperatures, but in the
temperature ranges where they work they are widely used.
Thermistors are temperature sensitive resistors.
All resistors vary with temperature, but thermistors are constructed of
semiconductor material with a
resistivity
that is especially sensitive to temperature. However, unlike most other
resistive devices, the resistance of a thermistor decreases with increasing
temperature. That's due to the properties of the semiconductor material
that the thermistor is made from. For some, that may be counterintuitive,
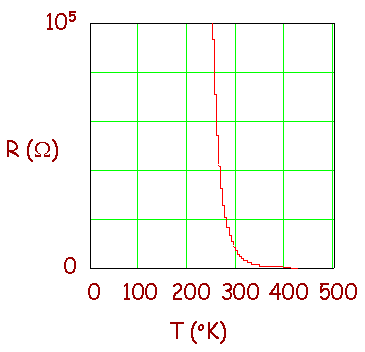
but it is correct. Here is a graph of resistance as a function of
temperature for a typical thermistor. Notice how the resistance drops from
100 kW , to a
very small value in a range around room temperature. Not only is the
resistance change in the opposite direction from what you expect, but the
magnitude of the percentage resistance change is substantial.
In this
lesson you will examine some of the characteristics of thermistors and the
circuits they are used in.

1/T = A + B*ln(R) + C*(ln(R))3 R in W,
T in oK
-
The constants, A, B and C can
be determined from experimental measurements of resistance, or they can be
calculated from tabular data.
Here are
some data points for a typical thermistor from "The Temperature Handbook" (Omega
Engineering, Inc., 1989). (By the way, when you refer to this thermistor,
you would say it has 5kW
at room temperature.)
|
T (oC)
|
R (W )
|
|
0
|
16,330
|
|
25
|
5000
|
|
50
|
1801
|
Using
these values, we can get three equations in A, B and C.
(1/273) = A + B
ln(16330) + C (ln(16330))3
(1/298) = A
+ B ln(5000) + C (ln(5000))3
(1/323) = A
+ B ln(1801) + C (ln(1801))3
This
set of simultaneous linear equations can be solved for A, B and C. Here
are the values computed for A, B and C.
A = 0.001284
B = 2.364x 10-4
C = 9.304x 10-8
Using these values you can compute the reciprocal,
and therefore the temperature, from a resistance measurement.
Using these values for A, B and C we obtain a
plot of resistance vs. Kelvin temperature.
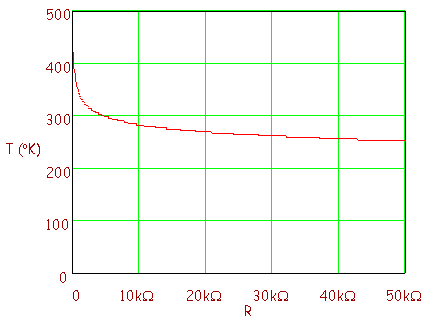
Getting
the temperature from resistance
If you
have a resistance value - and that is what you will measure electrically - you
then need to solve for the temperature. Use the reciprocal of the equation
above, and you will get:
T = 1/[A + B*ln(R) +
C*(ln(R))3] R in W,
T in oK
However, if the thermistor is embedded in a
circuit - like a voltage divider, for example - then you will have to measure
electrical quantities - usually voltage - and work back from that electrical
measurement.
There will be situations where you need to measure a higher temperature than a
thermistor can work in. Or you may need more precision than a thermistor
can give. Consider a thermocouple or and integrated circuit sensor like
the LM35.
How Do You Use A Thermistor?
Thermistors are most commonly used in bridge circuits like the one below.
Bridge circuits are discussed in more detail in the
lesson on bridge circuits.
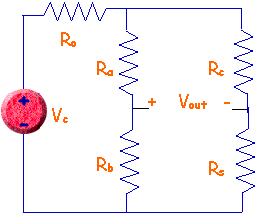
In this bridge circuit, three resistors are
constant, Ra, Rb, and Rc,
while the resistive sensor, Rs, varies depending upon some
physical variable - like temperature, light level, etc. That's where the
thermistor can be used.
The
thermistor can be placed anywhere in the bridge with three constant resistors,
but different placements can produce different behavior in the bridge. For
example, different placements might cause the output voltage to go in different
directions as the temperature changes.
|

