| Elementary Vector Analysis |
Elementary Vector Analysis
In order to measure many physical quantities, such as force or velocity, we
need to determine both a magnitude and a direction. Such quantities are
conveniently represented as vectors.
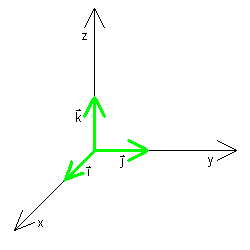
The direction of a vector v in 3-space is specified by its components in
the x, y, and z directions, respectively:
(x,y,z) or xi + yj + zk,
i = (1,0,0)
j = (0,1,0)
k = (0,0,1)
|
where i, j, and k are the coordinate vectors
along the x-, y-, and z-axes.
The magnitude of a vector v = (x,y,z), also called its length or
norm, is given by
Notes
Basic Operations on Vectors
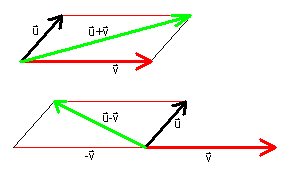
To add or subtract vectors u = (u1,u2,u3)
and v = (v1,v2,v3),
add or subtract the corresponding coordinates:
u + v = (u1+v1,u2+v2,u3+v3)
u - v = (u1-v1,u2-v2,u3-v3)
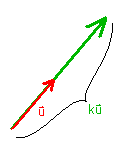
To mulitply vector u by a scalar k, multiply each coordinate of u
by k:
k u = (ku1,ku2,ku3)
Example
The vector v = (2,1,-2) = 2i + j - 2k has
magnitude
| ||
|
v |
||
= |
|
___________
�22 +12
-(-2)2
|
= 3. |
|
Thus, the vector 1/3v = (2/3,1/3,-2/3)
is a unit vector in the same direction as v.
In general, for v � 0, we can scale
(or normalize) v to the unit vector v/
||v|| pointing in the same direction as
v.
Dot Product
Let u = (u1,u2,u3) and v = (v1,v2,v3).
The dot product u � v (also called the scalar procuct
or Euclidean inner product) of u and v is defined in two
distinct (though equivalent) ways:
u � v=
u1v1+u2v2+u3v3
u � v is a number
�
�
� ||
u
|| ||
v
||
cosq
if
u �
0, v
�
0
0
if u = 0 or v
= 0
where 0 �
q
� p is the
angle between
u
and
v
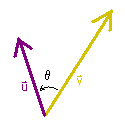
Properties of the Dot Product
- u � v = v � u
- u � (v + w) = (u � v) + (u �
w)
- u � u = || u
||2
See if you can verify each of these!
Example
If u = (1,-2,2) and v = (-4,0,2), then
Using the second definition of the dot product with ||
u || = 3 and ||
v || = 2�5,
so cosq = 0, yielding q
= p/2.
Though we might not have guessed it, u and v are perpendicular
to each other!
In general,
Two non-zero vectors u and v are perpendicular (or
orthogonal) if and only if u �v = 0.
Projection of a Vector
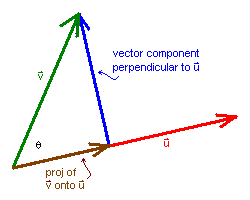
It is often useful to resolve a vector v into the sum of vector
components parallel and perpendicular to a vector u.
Consider first the parallel component, which is called the projection of v
onto u. This projection should be in the direction of u and should
have magnitude || v||cosq,
where 0 � q
� p is the angle between
u and v. Let's normalize u to u/||
u || and then scale this by the magnitude
|| v ||cosq:
| Projection of v onto u
|
|
| |
| = |
||v||
||u||
cosq
||u||2
|
u |
|
|
|
The perpendicular vector component of v is then just the difference
between v and the projection of v onto u.
In summary,
| projection of v onto u: |
|
vector component of v
perpendicular to u:
|
|
|
Cross Product
Let u = (u1,u2,u3) and v = (v1,v2,v3).
The cross product u � v yields a vector perpendicular to
both u and v with direction determined by the right-hand rule.
Specifically,
u � v = (u2v3-u3v2)i
- (u1v3-u3v1)j + (u1v2-u2v1)k
It can also be shown that
|| u � v
|| = || u
|| || v || sinq
for u � 0, for v
� 0
where 0 � q
� p is the angle between
u and v.
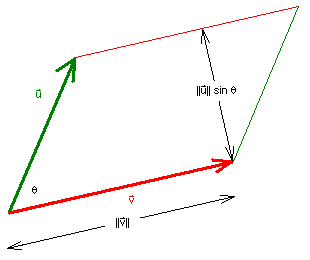
Thus, the magnitude || u �v
|| gives the area of the parallelogram formed by u
and v.
As implied by the geometric interpretation,
Non zero vectors u and v are parallel if and
only if u � v = 0.
Properties of the Cross Product
- u � v = - ( v � u)
- u � ( v + w ) = (u � v ) + ( u
� w )
- u � u = 0
Again, see if you can verify each of these.
In the following Exploration, select values for the components of u
and v. You will see u � v and u � v computed
and u, v, and u � v displayed on a coordinate
system.
Exploration
Key Concepts
Let u = (u1,u2,u3) and v = (v1,v2,v3).
- Basic Operations, Norm of a vector
- Dot Product
u
� v
nowrap="nowrap">u1v1+u2v2+u3v3 = �
�
� || u|| ||vvcosqif u
� 0, v
�
0
0u = 0 or v
= 0
where 0 �
q
�
p is the angle
between u and v
For u � 0, v
� 0, u � v = 0 if and only
if u is orthogonal to v.
- Projection of a Vector
| projection of v onto u: |
|
vector component of v
perpendicular to u:
|
|
- Cross Product
u � v = (u2v3-u3v2)i
- (u1v3-u3v1)j + (u1v2-u2v1)k
|| u � v ||
= || u || ||
v || sinq for u
� 0, for v �
0
where 0 � q
� p is the angle
between u and v.
For u � 0, v
� 0, u � v = 0 if and only
if u is parallel to v.
|

