Fourier Transform
The Fourier transform is a generalization of the
complex
Fourier series in the limit as
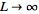 .
Replace the discrete .
Replace the discrete
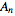 with the continuous
with the continuous
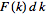 while letting
while letting
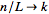 .
Then change the sum to an
integral,
and the equations become .
Then change the sum to an
integral,
and the equations become
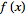
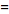
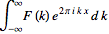
(1)
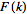
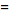
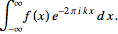
(2)
Here,
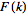
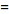
](/images/resistors/fourier-transform/Inline13.gif)
(3)

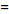
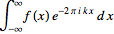
(4)
is called the forward (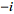 )
Fourier transform, and )
Fourier transform, and
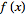
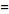
](/images/resistors/fourier-transform/Inline20.gif)
(5)

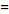
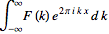
(6)
is called the inverse (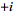 )
Fourier transform. The notation )
Fourier transform. The notation
](/images/resistors/fourier-transform/Inline25.gif) is introduced in Trott (2004, p. xxxiv), and
is introduced in Trott (2004, p. xxxiv), and
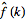 and
and
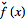 are sometimes also used to denote the Fourier transform and inverse Fourier
transform, respectively (Krantz 1999, p. 202).
are sometimes also used to denote the Fourier transform and inverse Fourier
transform, respectively (Krantz 1999, p. 202).
Note that some authors (especially physicists) prefer to write
the transform in terms of angular frequency
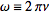 instead of the oscillation frequency
instead of the oscillation frequency
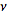 .
However, this destroys the symmetry, resulting in the transform pair .
However, this destroys the symmetry, resulting in the transform pair
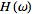
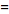
![F[h(t)]](/images/resistors/fourier-transform/Inline32.gif)
(7)

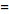
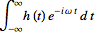
(8)
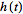
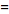
![F^(-1)[H(omega)]](/images/resistors/fourier-transform/Inline38.gif)
(9)

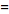
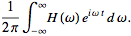
(10)
To restore the symmetry of the transforms, the convention
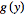
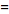
![F[f(t)]](/images/resistors/fourier-transform/Inline44.gif)
(11)

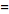
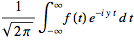
(12)
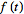
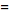
![F^(-1)[g(y)]](/images/resistors/fourier-transform/Inline50.gif)
(13)

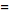
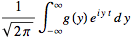
(14)
is sometimes used (Mathews and Walker 1970, p. 102).
In general, the Fourier transform pair may be defined using two
arbitrary constants
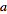 and
and
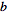 as
as
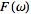
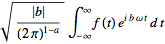
(15)
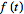
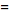
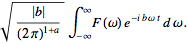
(16)
The Fourier transform
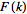 of a function
of a function
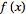 is implemented as
FourierTransform[f, x, k], and different choices
of
is implemented as
FourierTransform[f, x, k], and different choices
of
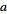 and
and
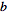 can be used by passing the optional FourierParameters->
can be used by passing the optional FourierParameters->
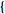 a,
b a,
b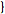 option. By default,
Mathematica takes FourierParameters as
option. By default,
Mathematica takes FourierParameters as
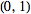 .
Unfortunately, a number of other conventions are in widespread use. For example, .
Unfortunately, a number of other conventions are in widespread use. For example,
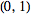 is used in modern physics,
is used in modern physics,
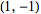 is used in pure mathematics and systems engineering,
is used in pure mathematics and systems engineering,
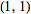 is used in probability theory for the computation of the
characteristic function,
is used in probability theory for the computation of the
characteristic function,
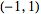 is used in classical physics, and
is used in classical physics, and
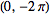 is used in signal processing. In this work, following Bracewell (1999, pp. 6-7),
it is always assumed that
is used in signal processing. In this work, following Bracewell (1999, pp. 6-7),
it is always assumed that
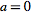 and
and
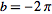 unless otherwise stated. This choice often results in greatly simplified
transforms of common functions such as 1,
unless otherwise stated. This choice often results in greatly simplified
transforms of common functions such as 1,
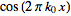 ,
etc. ,
etc.
Since any function can be split up into
even
and
odd portions
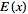 and
and
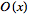 , ,
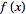
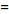
![1/2[f(x)+f(-x)]+1/2[f(x)-f(-x)]](/images/resistors/fourier-transform/Inline81.gif)
(17)

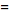
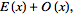
(18)
a Fourier transform can always be expressed in terms of the
Fourier cosine transform and
Fourier sine transform as
=int_(-infty)^inftyE(x)cos(2pikx)dx-iint_(-infty)^inftyO(x)sin(2pikx)dx.](/images/resistors/fourier-transform/NumberedEquation1.gif)
(19)
A function
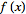 has a forward and inverse Fourier transform such that
has a forward and inverse Fourier transform such that
![f(x)={int_(-infty)^inftye^(2piikx)[int_(-infty)^inftyf(x)e^(-2piikx)dx]dk for f(x) continuous at x; 1/2[f(x_+)+f(x_-)] for f(x) discontinuous at x,](/images/resistors/fourier-transform/NumberedEquation2.gif)
(20)
provided that
1.
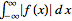 exists.
exists.
2. There are a finite number of discontinuities.
3. The function has bounded variation. A
sufficient weaker condition is fulfillment of the
Lipschitz condition
(Ramirez 1985, p. 29). The smoother a function (i.e., the larger
the number of continuous
derivatives), the more compact its Fourier transform.
The Fourier transform is linear, since if
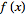 and
and
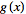 have Fourier transforms
have Fourier transforms
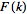 and
and
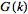 ,
then ,
then
Therefore,
The Fourier transform is also symmetric since
](/images/resistors/fourier-transform/Inline103.gif) implies
implies
](/images/resistors/fourier-transform/Inline104.gif) . .
Let
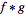 denote the
convolution, then the transforms of convolutions of functions have
particularly nice transforms,
denote the
convolution, then the transforms of convolutions of functions have
particularly nice transforms,
The first of these is derived as follows:
where
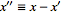 . .
There is also a somewhat surprising and extremely important
relationship between the
autocorrelation and the Fourier transform known as the
Wiener-Khinchin theorem. Let
=F(k)](/images/resistors/fourier-transform/Inline131.gif) ,
and ,
and
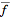 denote the
complex conjugate of
denote the
complex conjugate of
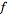 ,
then the Fourier transform of the
absolute square of ,
then the Fourier transform of the
absolute square of
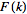 is given by
is given by
=int_(-infty)^inftyf^_(tau)f(tau+x)dtau.](/images/resistors/fourier-transform/NumberedEquation3.gif) |
(33)
|
The Fourier transform of a
derivative
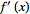 of a function
of a function
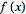 is simply related to the transform of the function
is simply related to the transform of the function
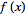 itself. Consider
itself. Consider
=int_(-infty)^inftyf^'(x)e^(-2piikx)dx.](/images/resistors/fourier-transform/NumberedEquation4.gif) |
(34)
|
Now use
integration by parts
![intvdu=[uv]-intudv](/images/resistors/fourier-transform/NumberedEquation5.gif) |
(35)
|
with
and
then
=[f(x)e^(-2piikx)]_(-infty)^infty-int_(-infty)^inftyf(x)(-2piike^(-2piikx)dx).](/images/resistors/fourier-transform/NumberedEquation6.gif) |
(40)
|
The first term consists of an oscillating function times
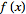 .
But if the function is bounded so that .
But if the function is bounded so that
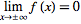 |
(41)
|
(as any physically significant signal must be), then the term
vanishes, leaving
This process can be iterated for the
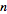 th
derivative to yield th
derivative to yield
=(2piik)^nF_x[f(x)](k).](/images/resistors/fourier-transform/NumberedEquation8.gif) |
(44)
|
The important
modulation theorem of Fourier transforms allows
](/images/resistors/fourier-transform/Inline158.gif) to be expressed in terms of
to be expressed in terms of
=F(k)](/images/resistors/fourier-transform/Inline159.gif) as follows,
as follows,
Since the
derivative of the Fourier transform is given by
=int_(-infty)^infty(-2piix)f(x)e^(-2piikx)dx,](/images/resistors/fourier-transform/NumberedEquation9.gif) |
(49)
|
it follows that
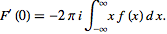 |
(50)
|
Iterating gives the general
formula
The
variance
of a Fourier transform is
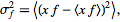 |
(53)
|
and it is true that
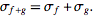 |
(54)
|
If
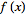 has the Fourier transform
has the Fourier transform
=F(k)](/images/resistors/fourier-transform/Inline179.gif) ,
then the Fourier transform has the shift property ,
then the Fourier transform has the shift property
so
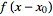 has the Fourier transform
has the Fourier transform
=e^(-2piikx_0)F(k).](/images/resistors/fourier-transform/NumberedEquation13.gif) |
(57)
|
If
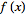 has a Fourier transform
has a Fourier transform
=F(k)](/images/resistors/fourier-transform/Inline188.gif) ,
then the Fourier transform obeys a similarity theorem. ,
then the Fourier transform obeys a similarity theorem.
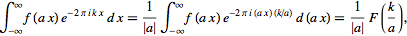 |
(58)
|
so
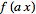 has the Fourier transform
has the Fourier transform
=|a|^(-1)F(k/a).](/images/resistors/fourier-transform/NumberedEquation15.gif) |
(59)
|
The "equivalent width" of a Fourier transform is
The "autocorrelation width" is
where
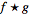 denotes the
cross-correlation of
denotes the
cross-correlation of
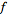 and
and
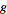 and
and
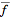 is the
complex conjugate.
is the
complex conjugate.
Any operation on
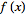 which leaves its
area
unchanged leaves
which leaves its
area
unchanged leaves
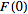 unchanged, since
unchanged, since
=F(0).](/images/resistors/fourier-transform/NumberedEquation16.gif) |
(64)
|
The following table summarized some common Fourier transform
pairs.
| Function |
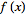 |
](/images/resistors/fourier-transform/Inline209.gif) |
|
Fourier transform--1 |
1 |
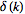 |
|
Fourier transform--cosine |
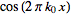 |
![1/2[delta(k-k_0)+delta(k+k_0)]](/images/resistors/fourier-transform/Inline212.gif) |
|
Fourier transform--delta function |
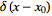 |
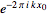 |
|
Fourier transform--exponential function |
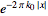 |
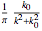 |
|
Fourier transform--Gaussian |
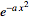 |
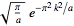 |
|
Fourier transform--Heaviside step function |
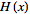 |
![1/2[delta(k)-i/(pik)]](/images/resistors/fourier-transform/Inline220.gif) |
|
Fourier transform--inverse function |
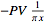 |
![i[1-2H(-k)]](/images/resistors/fourier-transform/Inline222.gif) |
|
Fourier transform--Lorentzian function |
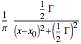 |
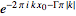 |
|
Fourier transform--ramp function |
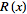 |
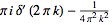 |
|
Fourier transform--sine |
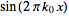 |
![1/2i[delta(k+k_0)-delta(k-k_0)]](/images/resistors/fourier-transform/Inline228.gif) |
In two dimensions, the Fourier transform becomes
Similarly, the
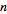 -dimensional
Fourier transform can be defined for -dimensional
Fourier transform can be defined for
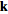 , ,
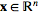 by
by
|

