Laplace Transform
The Laplace transform is an
integral transform perhaps second only to the
Fourier transform in its utility in solving physical problems. The Laplace
transform is particularly useful in solving linear
ordinary differential equations such as those arising in the analysis of
electronic circuits.
The (unilateral) Laplace transform
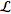 (not to be confused with the
Lie
derivative, also commonly denoted
(not to be confused with the
Lie
derivative, also commonly denoted
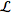 )
is defined by )
is defined by
=int_0^inftyf(t)e^(-st)dt,](/images/resistors/laplace-transform/NumberedEquation1.gif) |
(1)
|
where
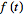 is defined for
is defined for
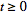 (Abramowitz and Stegun 1972). The unilateral Laplace transform is almost always
what is meant by "the" Laplace transform, although a
bilateral Laplace transformm is sometimes also defined as
(Abramowitz and Stegun 1972). The unilateral Laplace transform is almost always
what is meant by "the" Laplace transform, although a
bilateral Laplace transformm is sometimes also defined as
=int_(-infty)^inftyf(t)e^(-st)dt](/images/resistors/laplace-transform/NumberedEquation2.gif) |
(2)
|
(Oppenheim et al. 1997). The unilateral Laplace transform
](/images/resistors/laplace-transform/Inline5.gif) is implemented in
Mathematica as
LaplaceTransform[f[t], t, s].
is implemented in
Mathematica as
LaplaceTransform[f[t], t, s].
The inverse Laplace transform is known as the
Bromwich integral, sometimes known as the Fourier-Mellin integral (see also
the related
Duhamel's convolution principle).
A table of several important one-sided Laplace transforms is
given below.
In the above table,
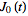 is the zeroth-order
Bessel function of the first kind,
is the zeroth-order
Bessel function of the first kind,
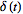 is the
delta function, and
is the
delta function, and
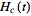 is the
Heaviside step function.
is the
Heaviside step function.
The Laplace transform has many important properties. The Laplace
transform existence theorem states that, if
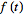 is
piecewise continuous on every finite interval in
is
piecewise continuous on every finite interval in
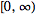 satisfying
satisfying
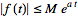 |
(3)
|
for all
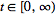 ,
then ,
then
](/images/resistors/laplace-transform/Inline52.gif) exists for all
exists for all
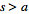 .
The Laplace transform is also
unique,
in the sense that, given two functions .
The Laplace transform is also
unique,
in the sense that, given two functions
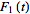 and
and
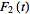 with the same transform so that
with the same transform so that
=L_t[F_2(t)](s)=f(s),](/images/resistors/laplace-transform/NumberedEquation4.gif) |
(4)
|
then
Lerch's theorem guarantees that the integral
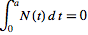 |
(5)
|
vanishes for all
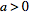 for a
null function defined by
for a
null function defined by
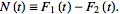 |
(6)
|
The Laplace transform is
linear since
The Laplace transform of a
convolution is given by
![L_t[f(t)*g(t)]=L_t[f(t)]L_t[g(t)]](/images/resistors/laplace-transform/Inline66.gif) |
(10)
|
![L_t^(-1)[FG]=L_t^(-1)[F]*L_t^(-1)[G].](/images/resistors/laplace-transform/Inline67.gif) |
(11)
|
Now consider
differentiation. Let
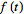 be continuously differentiable
be continuously differentiable
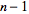 times in
times in
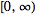 .
If .
If
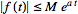 ,
then ,
then
=s^nL_t[f(t)]-s^(n-1)f(0)-s^(n-2)f^'(0)-...-f^((n-1))(0).](/images/resistors/laplace-transform/NumberedEquation7.gif) |
(12)
|
This can be proved by
integration by parts,
Continuing for higher-order derivatives then gives
=s^2L_t[f(t)](s)-sf(0)-f^'(0).](/images/resistors/laplace-transform/NumberedEquation8.gif) |
(19)
|
This property can be used to transform differential equations
into algebraic equations, a procedure known as the
Heaviside calculus, which can then be inverse transformed to obtain the
solution. For example, applying the Laplace transform to the equation
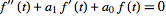 |
(20)
|
gives
-sf(0)-f^'(0)}+a_1{sL_t[f(t)](s)-f(0)}+a_0L_t[f(t)](s)=0](/images/resistors/laplace-transform/NumberedEquation10.gif) |
(21)
|
(s^2+a_1s+a_0)-sf(0)-f^'(0)-a_1f(0)=0,](/images/resistors/laplace-transform/NumberedEquation11.gif) |
(22)
|
which can be rearranged to
=(sf(0)+f^'(0)+a_1f(0))/(s^2+a_1s+a_0).](/images/resistors/laplace-transform/NumberedEquation12.gif) |
(23)
|
If this equation can be inverse Laplace transformed, then the
original differential equation is solved.
The Laplace transform satisfied a number of useful properties.
Consider
exponentiation. If
=F(s)](/images/resistors/laplace-transform/Inline88.gif) for
for
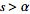 (i.e.,
(i.e.,
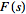 is the Laplace transform of
is the Laplace transform of
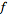 ),
then ),
then
=F(s-a)](/images/resistors/laplace-transform/Inline92.gif) for
for
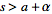 .
This follows from .
This follows from
The Laplace transform also has nice properties when applied to
integrals
of functions. If
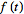 is
piecewise continuous and
is
piecewise continuous and
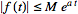 ,
then ,
then
![L_t[int_0^tf(t^')dt^']=1/sL_t[f(t)](s).](/images/resistors/laplace-transform/NumberedEquation13.gif) |
(27)
|
|