The (unilateral)
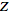 -transform
of a sequence -transform
of a sequence
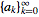 is defined as
is defined as
=sum_(k=0)^infty(a_k)/(z^k).](/images/resistors/z-transform/NumberedEquation1.gif) |
(1)
|
This definition is implemented in
Mathematica as
ZTransform[a, n, z]. Similarly, the inverse
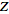 -transform
is implemented as
InverseZTransform[A, z, n]. -transform
is implemented as
InverseZTransform[A, z, n].
"The"
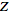 -transform
generally refers to the
unilateral Z-transform. Unfortunately, there are a number of other
conventions. Bracewell (1999) uses the term " -transform
generally refers to the
unilateral Z-transform. Unfortunately, there are a number of other
conventions. Bracewell (1999) uses the term "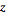 -transform"
(with a lower case -transform"
(with a lower case
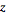 )
to refer to the unilateral )
to refer to the unilateral
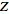 -transform.
Girling (1987, p. 425) defines the transform in terms of samples of a continuous
function. Worse yet, some authors define the -transform.
Girling (1987, p. 425) defines the transform in terms of samples of a continuous
function. Worse yet, some authors define the
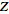 -transform
as the
bilateral Z-transform. -transform
as the
bilateral Z-transform.
In general, the inverse
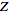 -transform
of a sequence is not unique unless its region of convergence is specified
(Zwillinger 1996, p. 545). If the -transform
of a sequence is not unique unless its region of convergence is specified
(Zwillinger 1996, p. 545). If the
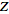 -transform -transform
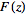 of a function is known analytically, the inverse
of a function is known analytically, the inverse
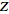 -transform -transform
](/images/resistors/z-transform/Inline13.gif) can be computed using the
contour integral
can be computed using the
contour integral
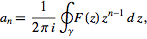 |
(2)
|
where
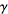 is a closed contour surrounding the origin of the
complex plane in the domain of analyticity of
is a closed contour surrounding the origin of the
complex plane in the domain of analyticity of
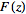 (Zwillinger 1996, p. 545)
(Zwillinger 1996, p. 545)
The unilateral transform is important in many applications
because the
generating function
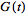 of a sequence of numbers
of a sequence of numbers
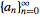 is given precisely by
is given precisely by
)](/images/resistors/z-transform/Inline18.gif) ,
the ,
the
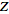 -transform
of -transform
of
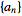 in the variable
in the variable
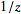 (Germundsson 2000). In other words, the inverse
(Germundsson 2000). In other words, the inverse
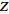 -transform
of a function -transform
of a function
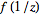 gives precisely the sequence of terms in the series expansion of
gives precisely the sequence of terms in the series expansion of
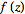 .
So, for example, the terms of the series of .
So, for example, the terms of the series of
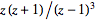 are given by
are given by
=Z^(-1)[-(y(y+1))/((y-1)^3)](n)=n^2.](/images/resistors/z-transform/NumberedEquation3.gif) |
(3)
|
Girling (1987) defines a variant of the unilateral
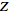 -transform
that operates on a continuous function -transform
that operates on a continuous function
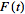 sampled at regular intervals
sampled at regular intervals
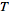 , ,
=L_t[F^*(t)](z),](/images/resistors/z-transform/NumberedEquation4.gif) |
(4)
|
where
](/images/resistors/z-transform/Inline29.gif) is the
Laplace transformm,
is the
Laplace transformm,
the one-sided
shah
function with period
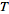 is given by
is given by
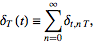 |
(7)
|
and
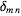 is the
Kronecker delta, giving
is the
Kronecker delta, giving
=sum_(n=0)^infty(F(nT))/(z^n).](/images/resistors/z-transform/NumberedEquation6.gif) |
(8)
|
An alternative equivalent definition is
=sum_(residues)(1/(1-e^(Tz)z^(-1)))f(z),](/images/resistors/z-transform/NumberedEquation7.gif) |
(9)
|
where
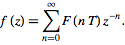 |
(10)
|
This definition is essentially equivalent to the usual one by
taking
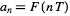 . .
The following table summarizes the
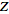 -transforms
for some common functions (Girling 1987, pp. 426-427; Bracewell 1999). Here, -transforms
for some common functions (Girling 1987, pp. 426-427; Bracewell 1999). Here,
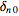 is the
Kronecker delta,
is the
Kronecker delta,
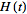 is the
Heaviside step function, and
is the
Heaviside step function, and
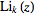 is the
polylogarithm.
is the
polylogarithm.
The
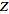 -transform
of the general power function -transform
of the general power function
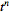 can be computed analytically as
can be computed analytically as
where the
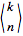 are
Eulerian numbers and
are
Eulerian numbers and
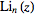 is a
polylogarithm. Amazingly, the
is a
polylogarithm. Amazingly, the
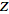 -transforms
of -transforms
of
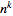 are therefore generators for
Euler's number triangle.
are therefore generators for
Euler's number triangle.
The
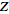 -transform -transform
=F(z)](/images/resistors/z-transform/Inline89.gif) satisfies a number of important properties, including linearity
satisfies a number of important properties, including linearity
=aZ[{a_n}](z)+bZ[{b_n}](z),](/images/resistors/z-transform/NumberedEquation9.gif) |
(14)
|
translation
scaling
=F(z/b),](/images/resistors/z-transform/NumberedEquation10.gif) |
(19)
|
and multiplication by powers of
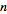
(Girling 1987, p. 425; Zwillinger 1996, p. 544).
The
discrete Fourier transform is a special case of the
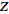 -transform
with -transform
with
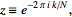 |
(22)
|
and a
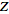 -transform
with -transform
with
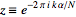 |
(23)
|
for
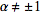 is called a
fractional Fourier transform.
is called a
fractional Fourier transform.
|