Commutative rings, in general
The examples to keep in mind are these: the set of integers Z; the set
Zn of integers modulo n; any field F (in particular the set Q
of rational numbers and the set R of real numbers); the set F[x] of all
polynomials with coefficients in a field F. The axioms are similar to those for
a field, but the requirement that each nonzero element has a multiplicative
inverse is dropped, in order to include integers and polynomials in the class of
objects under study.
5.1.1. Definition Let R be a set on which two binary operations are
defined, called addition and multiplication, and denoted by + and �. Then
R is called a commutative ring with respect to these operations if the
following properties hold:
(i) Closure: If a,b
 R, then the
sum a+b and the product a�b are uniquely defined and belong to R. R, then the
sum a+b and the product a�b are uniquely defined and belong to R.
(ii) Associative laws: For all a,b,c
 R, R,
a+(b+c) = (a+b)+c and a�(b�c) = (a�b)�c.
(iii) Commutative laws: For all a,b
 R, R,
a+b = b+a and a�b = b�a.
(iv) Distributive laws: For all a,b,c
 R, R,
a�(b+c) = a�b + a�c and (a+b)�c =
a�c + b�c.
(v) Additive identity: The set R contains an additive
identity element, denoted by 0, such that for all a
 R, R,
a+0 = a and 0+a = a.
(vi) Additive inverses: For each a
 R, the
equations R, the
equations
a+x = 0 and x+a = 0
have a solution x
 R, called the
additive inverse of a, and denoted by -a. R, called the
additive inverse of a, and denoted by -a.
The commutative ring R is called a commutative ring with identity if it
contains an element 1, assumed to be different from 0, such that for all a
 R, R,
a�1 = a and 1�a = a.
In this case, 1 is called a multiplicative identity element or, more
generally, simply an identity element.
As with groups, we will use juxtaposition to indicate multiplication, so that
we will write ab instead of a�b.
Example 5.1.1. (Zn) The rings Zn
form a class of commutative rings that is a good source of examples and
counterexamples.
5.1.2. Definition Let S be a commutative ring. A nonempty subset R of
S is called a subring of S if it is a commutative ring under the addition
and multiplication of S.
5.1.3. Proposition Let S be a commutative ring, and let R be a
nonempty subset of S. Then R is a subring of S if and only if
- (i) R is closed under addition and multiplication; and
- (ii) if a
 R, then
-a R, then
-a  R. R.
5.1.4. Definition Let R be a commutative ring with identity element 1. An
element a  R
is said to be invertible if there exists an element b R
is said to be invertible if there exists an element b
 R such that
ab = 1. The element a is also called a unit of R, and its multiplicative
inverse is usually denoted by a-1. R such that
ab = 1. The element a is also called a unit of R, and its multiplicative
inverse is usually denoted by a-1.
5.1.5. Proposition Let R be a commutative ring with identity. Then the
set R� of units of R is an abelian group under the multiplication of
R.
An element e of a commutative ring R is said to be idempotent if e2
= e. An element a is said to be nilpotent if there exists a positive
integer n with an = 0.
5.2.1. Definition Let R and S be commutative rings. A function
 :R->S is
called a ring homomorphism if :R->S is
called a ring homomorphism if
 (a+b) = (a+b) =
 (a) + (a) +
 (b) and (b) and
 (ab) = (ab) =
 (a) (a) (b) (b)
for all a,b  R.
R.
A ring homomorphism that is one-to-one and onto is called an isomorphism.
If there is an isomorphism from R onto S, we say that R is isomorphic to
S, and write R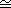 S.
An isomorphism from the commutative ring R onto itself is called an
automorphism of R. S.
An isomorphism from the commutative ring R onto itself is called an
automorphism of R.
5.2.2. Proposition
- (a) The inverse of a ring isomorphism is a ring isomorphism.
- (b) The composition of two ring isomorphisms is a ring
isomorphism.
5.2.3. Proposition Let
 :R->S be a
ring homomorphism. Then :R->S be a
ring homomorphism. Then
- (a)
 (0) =
0; (0) =
0;
- (b)
 (-a) =
- (-a) =
- (a)
for all a in R; (a)
for all a in R;
- (c) if R has an identity 1, then
 (1) is
idempotent; (1) is
idempotent;
- (d)
 (R) is
a subring of S. (R) is
a subring of S.
5.2.4. Definition Let
 :R->S be a
ring homomorphism. The set :R->S be a
ring homomorphism. The set
{ a
 R | R |
 (a) = 0 } (a) = 0 }
is called the kernel of
 , denoted
by ker( , denoted
by ker( ). ).
5.2.5. Proposition Let
 :R->S be a
ring homomorphism. :R->S be a
ring homomorphism.
- (a) If a,b
 ker( ker( )
and r )
and r  R,
then a+b, a-b, and ra belong to ker( R,
then a+b, a-b, and ra belong to ker( ). ).
- (b) The homomorphism
 is an
isomorphism if and only if ker( is an
isomorphism if and only if ker( )
= {0} and )
= {0} and
 (R) =
S. (R) =
S.
Example 5.2.5. Let R and S be commutative rings, let
 :R->S be a
ring homomorphism, and let s be any element of S. Then there exists a unique
ring homomorphism :R->S be a
ring homomorphism, and let s be any element of S. Then there exists a unique
ring homomorphism
 :R[x]->S such
that :R[x]->S such
that
 (r) = (r) =
 (r) for all r (r) for all r
 R and R and
 (x) = s,
defined by (x) = s,
defined by
 (a0
+ a1x + ... + amxm) = (a0
+ a1x + ... + amxm) =
 (a0)
+ (a0)
+  (a1)s
+ ... + (a1)s
+ ... +  (am)sm. (am)sm.
5.2.7. Proposition Let R and S be commutative rings. The set of
ordered pairs (r,s) such that r
 R and s R and s
 S is a
commutative ring under componentwise addition and multiplication. S is a
commutative ring under componentwise addition and multiplication.
5.2.8. Definition Let R and S be commutative rings. The set of ordered
pairs (r,s) such that r
 R and s R and s
 S is called
the direct sum of R and S. S is called
the direct sum of R and S.
Example 5.2.10. The ring Zn is isomorphic to the
direct sum of the rings Zk that arise in the prime
factorization of n. This describes the structure of Zn in
terms of simpler rings, and is the first example of what is usually called a
``structure theorem.'' This structure theorem can be used to determine the
invertible, idempotent, and nilpotent elements of Zn and
provides an easy proof of our earlier formula for the Euler phi-function in
terms of the prime factors of n.
5.2.9. Definition Let R be a commutative ring with identity. The
smallest positive integer n such that (n)(1) = 0 is called the characteristic
of R, denoted by char(R). If no such positive integer exists, then R is said to
have characteristic zero.
Ideals and factor rings
5.3.1. Definition Let R be a commutative ring. A nonempty subset I of R
is called an ideal of R if
- (i) a � b
 I for all
a,b I for all
a,b  I,
and I,
and
- (ii) ra
 I, for
all a I, for
all a  I
and r I
and r  R. R.
5.3.2. Proposition Let R be a commutative ring with identity. Then R is a
field if and only if it has no proper nontrivial ideals.
5.3.8. Definition Let I be a proper ideal of the commutative ring R.
Then I is said to be a prime ideal of R if for all a,b
 R it is true
that ab R it is true
that ab  I
implies a I
implies a  I
or b I
or b  I. I.
The ideal I is said to be a maximal ideal of R if for all ideals J of R
such that I
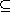 J J
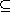 R,
either J = I or J = R. R,
either J = I or J = R.
For an ideal I of a commutative ring R, the set { a+I | a R
} of cosets
of I in R (under addition) is denoted by R/I. By
Theorem 3.8.4,
the set forms a group under addition. The next theorem justifies calling R/I the
factor ring of R modulo I. R
} of cosets
of I in R (under addition) is denoted by R/I. By
Theorem 3.8.4,
the set forms a group under addition. The next theorem justifies calling R/I the
factor ring of R modulo I.
5.3.6. Theorem If I is an ideal of the commutative ring R, then R/I is
a commutative ring, under the operations
(a+I) + (b+I) = (a+b) + I and (a+I)(b+I) = ab + I,
for all a,b  R.
R.
5.3.7. Proposition Let I be an ideal of the commutative ring R.
- (a) The natural projection mapping
 :R->R/I
defined by :R->R/I
defined by  (a)
= a+I for all a (a)
= a+I for all a
 R is a
ring homomorphism, and ker( R is a
ring homomorphism, and ker( )
= I. )
= I.
- (b) There is a one-to-one correspondence between the ideals of
R/I and the ideals of R that contain I.
5.2.6. Theorem [Fundamental Homomorphism Theorem for Rings] Let
 :R->S be a
ring homomorphism. Then R/ker( :R->S be a
ring homomorphism. Then R/ker( )
is isomorphic to )
is isomorphic to
 (R). (R).
Integral domains
5.1.6. Definition A commutative ring R with identity is called an
integral domain if for all a,b
 R, ab = 0
implies a = 0 or b = 0. R, ab = 0
implies a = 0 or b = 0.
The ring of integers Z is the most fundamental example of an integral
domain. The ring of all polynomials with real coefficients is also an integral
domain, but the larger ring of all real valued functions is not an integral
domain.
The cancellation law for multiplication holds in R if and only if R has no
nonzero divisors of zero. One way in which the cancellation law holds in R is if
nonzero elements have inverses in a larger ring; the next two results
characterize integral domains as subrings of fields (that contain the identity
1).
5.1.7. Theorem Let F be a field with identity 1. Any subring of F that
contains 1 is an integral domain.
5.4.4. Theorem Let D be an integral domain. Then there exists a field
F that contains a subring isomorphic to D.
5.1.8. Theorem Any finite integral domain must be a field.
5.2.10. Proposition An integral domain has characteristic 0 or p, for
some prime number p.
5.3.9. Proposition Let I be a proper ideal of the commutative ring R
with identity.
- (a) The factor ring R/I is a field if and only if I is a
maximal ideal
of R.
- (b) The factor ring R/I is a integral domain if and only if I is
a prime ideal
of R.
- (c) If I is maximal, then it is a prime ideal.
5.3.3. Definition Let R be a commutative ring with identity, and let a
 R. The ideal R. The ideal
Ra = { x
 R | x = ra
for some r R | x = ra
for some r  R
} R
}
is called the principal ideal generated by a.
An integral domain in which every ideal is a principal ideal is called a
principal ideal domain.
Example 5.3.1. (Z is a principal ideal domain)
Theorem 1.1.4
shows that the ring of integers Z is a principal ideal domain. Moreover,
given any nonzero ideal I of Z, the smallest positive integer in I is a
generator for the ideal.
5.3.10. Theorem Every nonzero prime ideal of a principal ideal domain
is maximal.
Example 5.3.7. (Ideals of F[x]) Let F be any field. Then F[x] is a
principal ideal domain, since by
Theorem
4.2.2 the ideals of F[x] have the form I = <f(x)>, where f(x) is the unique
monic polynomial of minimal degree in the ideal. The ideal I is prime (and hence
maximal) if and only if f(x) is irreducible. If p(x) is irreducible, then the
factor ring F[x]/<p(x)> is a field.
Example 5.3.8. (Evaluation mapping) Let F be a subfield of E, and for
any element u  E define the evaluation mapping
E define the evaluation mapping
 u:F[x]->E
by u:F[x]->E
by  u(g(x))
= g(u), for all g(x) u(g(x))
= g(u), for all g(x)
 F[x]. Since F[x]. Since
 u(F[x])
is a subring of E that contains 1, it is an integral domain, and so the kernel
of u(F[x])
is a subring of E that contains 1, it is an integral domain, and so the kernel
of  u
is a prime ideal. Thus if the kernel is nonzero, then it is a maximal ideal, so
F[x]/ker( u
is a prime ideal. Thus if the kernel is nonzero, then it is a maximal ideal, so
F[x]/ker( u)
is a field, and the image of u)
is a field, and the image of
 u
is a subfield of E. u
is a subfield of E.
|

