Composition series
10.4.1. Definition. A composition series of length n for a nonzero
module M is a chain of n+1 submodules
M = M0
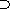 M1 M1
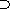 . . . . . .
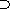 Mn
= (0) Mn
= (0)
such that Mi-1/Mi is a simple module for i=1,2,...,n.
These simple modules are called the composition factors of the series.
10.4.2. Theorem. [Jordan-Holder] If a module M has a composition
series, then any other composition series for M is equivalent to it.
As an immediate consequence of the Jordan-Holder theorem, if a module RM
has a composition series, then all composition series for M must have the same
length, which we denote by
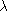 (M). (M).
This
is called the length of the module, and we simply say that the module has
finite length. Since any ascending chain of submodules can be refined to
a composition series,
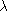 (M) gives
a uniform bound on the number of terms in any properly ascending chain of
submodules. We also note that if M1 and M2 have finite
length, then (M) gives
a uniform bound on the number of terms in any properly ascending chain of
submodules. We also note that if M1 and M2 have finite
length, then
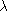 (M1 (M1
 M2)
= M2)
= 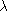 (M1)
+ (M1)
+ 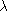 (M2). (M2).
10.4.3. Proposition. A module has finite length if and only if it is
both Artinian and Noetherian.
A module RM is said to be indecomposable if its only direct
summands are (0) and M. As our first example, we note that Z is
indecomposable as a module over itself, since the intersection of any two
nonzero ideals is again nonzero. To give additional examples of indecomposable
Z-modules, recall any finite abelian group is isomorphic to a
direct sum of cyclic groups of prime power order. Using this result, we see that
a finite Z-module is indecomposable if and only if it is
isomorphic to Zn, where n=pk for some
prime p.
10.4.4. Proposition. If RM has finite length, then there
exist finitely many indecomposable submodules M1, M2, . .
. , Mn such that
M = M1
 M2 M2
 .
. . .
. .
 Mn. Mn.
10.4.5. Lemma. [Fitting] Let M be a module with length n, and let f be an
endomorphism of M. Then
M = Im (fn)
 ker(fn)
. ker(fn)
.
10.4.6. Proposition. Let M be an indecomposable module of finite length.
Then for any endomorphism f of M the following conditions are equivalent.
(1) f is one-to-one;
(2) f is onto;
(3) f is an automorphism;
(4) f is not nilpotent.
10.4.7. Proposition. Let M be an indecomposable module of finite
length, and let f1, f2 be endomorphisms of M. If f1
+ f2 is an automorphism, then either f1 or f2
is an automorphism.
10.4.8. Lemma. Let X1, X2, Y1, Y2
be left R-modules, and let f: X1
 X2
-> Y1 X2
-> Y1
 Y2
be an isomorphism. Let i1 : X1 -> X1 Y2
be an isomorphism. Let i1 : X1 -> X1
 X2
and i2 : X2 -> X1 X2
and i2 : X2 -> X1
 X2
be the natural inclusion maps, and let p1 : Y1 X2
be the natural inclusion maps, and let p1 : Y1
 Y2
-> Y1 and p2 : Y1 Y2
-> Y1 and p2 : Y1
 Y2
-> Y2 be the natural projections. If p1 f i1 :
X1 -> Y1 is an isomorphism, then p2 f i2
: X2 -> Y2 is an isomorphism. Y2
-> Y2 be the natural projections. If p1 f i1 :
X1 -> Y1 is an isomorphism, then p2 f i2
: X2 -> Y2 is an isomorphism.
10.4.9. Theorem. [Krull-Schmidt] Let {Xj}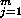 and {Yi}
and {Yi}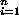 be indecomposable left R-modules of finite length. If
be indecomposable left R-modules of finite length. If
X1
 .
. . .
. .
 Xm Xm
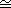 Y1 Y1
 .
. . .
. .
 Yn, Yn,
then m = n and there exists a permutation
  Sn
with Sn
with  (j)=i and
Xj (j)=i and
Xj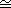 Yi,
for 1 Yi,
for 1 j j m. m.
Semisimple modules
10.5.1. Definition. Let M be a left R-module. The sum of all minimal
submodules of M is called the socle of M, and is denoted by Soc(M). The
module M is called semisimple if it can be expressed as a sum of minimal
submodules.
A semisimple module R M behaves like a vector space in that any
submodule splits off, or equivalently, that any submodule N has a complement
N' such that N+N'=M and N N'=0. N'=0.
10.5.2. Theorem. Any submodule of a semisimple module has a complement
that is a direct sum of minimal submodules.
10.5.3. Corollary. The following conditions are equivalent for a
module R M.
(1) M is semisimple;
(2) Soc (M) = M.
(3) M is completely reducible;
(4) M is isomorphic to a direct sum of simple modules.
10.5.4. Corollary. Every vector space over a division ring has a
basis.
10.5.5. Definition. The module RQ is said to be
injective if for each one-to-one R-homomorphism i:RM->RN
and each R-homomorphism f:M->Q there exists an R-homomorphism f*:N->Q such that
f*i=f.
10.5.6. Theorem. The following conditions are equivalent for the ring
R.
(1) R is a direct sum of finitely many minimal left ideals;
(2) R R is a semisimple module;
(3) every left R-module is semisimple;
(4) every left R-module is projective;
(5) every left R-module is injective;
(6) every left R-module is completely reducible.
10.5.7. Corollary. Let D be a division ring, and let R be the ring Mn(D)
of all n�n matrices over D. Then every left R-module is completely reducible.
Let R be a ring, and let G be a group. The group ring RG is defined to
be a free left R-module with the elements of G as a basis. The multiplication on
RG is defined by
( w w G
aw w ) ( G
aw w ) ( x
x G
bx x ) = G
bx x ) =
 z z G
cz z where cz = G
cz z where cz =
 z=wx
aw bx. z=wx
aw bx.
The crucial property of a group ring is that it converts group homomorphisms
from G into the group of units of a ring into ring homomorphisms. To be more
precise, let S be a ring,
let 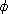 :G->Sx
be a group homomorphism, :G->Sx
be a group homomorphism,
and let 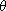 :R->Z(S)
be any ring homomorphism. :R->Z(S)
be any ring homomorphism.
(Recall that Sx denotes the group of invertible elements of S and
Z(S) denotes the center of S.)
Then there is a unique ring homomorphism
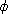 :RG->S such
that :RG->S such
that
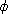 (g)= (g)=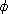 (g)
for all g (g)
for all g G and G and
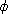 (r)= (r)=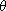 (r)
for all r (r)
for all r R. R.
10.5.8. Theorem. [Maschke] Let G be a finite group and let K be a
field such that |G| is not divisible by chr(K). Then every KG-module is
completely reducible.
10.5.9. Theorem. [Baer's criterion] For any left R-module Q, the
following conditions are equivalent.
(1) The module Q is injective;
(2) for each left ideal A of R and each R-homomorphism f:A->Q there
exists an extension f*:R->Q such that f*(a)=f(a) for all a A; A;
(3) for each left ideal A of R and each R-homomorphism f:A->Q there
exists q Q such
that f(a)=aq, for all a Q such
that f(a)=aq, for all a A. A.
10.5.10. Proposition. Let D be a principal ideal domain, with quotient
field Q.
(a) The module DQ is injective.
(b) Let I be any nonzero ideal of D, and let R be the ring D/I. Then R is
an injective module, when regarded as an R-module.
Tensor products
We need to begin with the definition of a bilinear function. Given modules MR
and RN over a ring R and an abelian group A, a function
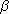 : M � N ->
A is said to be R-bilinear if : M � N ->
A is said to be R-bilinear if
(i) 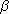 ( x1
+ x2 , y ) = ( x1
+ x2 , y ) =
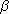 ( x1
, y ) + ( x1
, y ) + 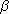 ( x2
, y ); ( x2
, y );
(ii) 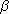 ( x ,
y1 + y2 ) = ( x ,
y1 + y2 ) =
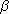 ( x , y1
) + ( x , y1
) + 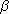 ( x , y2
); ( x , y2
);
(iii) 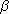 ( xr,
y ) = ( xr,
y ) = 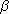 ( x ,
ry ) ( x ,
ry )
for all x, x1, x2
 M, y, y1,
y2 M, y, y1,
y2  N
and r N
and r R. R.
10.6.1. Definition. A tensor product of the modules MR
and RN is an abelian group T(M,N) and an R-bilinear map
 : M � N ->
T(M,N) such that for any abelian group A and any R-bilinear map : M � N ->
T(M,N) such that for any abelian group A and any R-bilinear map
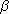 : M � N ->
A there exists a unique Z-homomorphism f:T(M,N)->A such that f : M � N ->
A there exists a unique Z-homomorphism f:T(M,N)->A such that f = =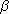 . .
The group T(M,N) is usually denoted by M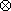 RN,
and for x RN,
and for x M, y M, y N
the image N
the image  (x,y)
is denoted by x (x,y)
is denoted by x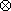 y. y.
10.6.2. Proposition. Let MR and RN be modules.
The tensor product M RN
is unique up to isomorphism, if it exists. RN
is unique up to isomorphism, if it exists.
10.6.3. Proposition. For any modules MR and RN,
the tensor product M RN
exists. RN
exists.
10.6.4. Proposition. Let M, M' be right R-modules, let N, N' be left
R-modules, and let f Hom(MR,M'R)
and g Hom(MR,M'R)
and g Hom(RN,RN'). Hom(RN,RN').
(a) Then there is a unique Z-homomorphism f g:M g:M RN->M' RN->M'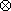 RN' RN'
with (f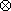 g)
(x g)
(x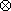 y) =
f(x) y) =
f(x) 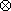 g(y)
for all x g(y)
for all x M, y M, y
 N. N.
(b) If f and g are onto, then f g
is onto, and ker(f g
is onto, and ker(f g)
is generated by all elements of the form x g)
is generated by all elements of the form x y
such that either x y
such that either x ker(f)
or y ker(f)
or y ker(g). ker(g).
10.6.5. Proposition. Let MR be a right R-module, and let {N } }
  I be a collection of left R-modules. Then
I be a collection of left R-modules. Then
M
 R
( R
( 
  I N
I N ) )
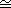
 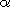  I ( M
I ( M
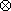 R
N R
N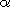 ). ).
10.6.6. Definition. Let R and S be rings, and let U be a left S-module.
If U is also a right R-module such that (sx)r = s(xr) for all s
 S, r S, r
 R, and x R, and x
 U, then U is
called an S-R-bimodule. U, then U is
called an S-R-bimodule.
If U is an S-R-bimodule we use the notation SUR.
10.6.7. Proposition. Let R, S, and T be rings, and let SUR,
RMT , and SNT be bimodules.
(a) The tensor product U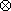 R
M is a bimodule, over S on the left and T on the right. R
M is a bimodule, over S on the left and T on the right.
(b) The set HomS(U,N) is a bimodule, over R on the left and T
on the right.
10.6.8. Proposition. Let M be a left R-module, and let N be a left
S-module.
(a) R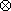 RM RM
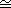 M, as left
R-modules. M, as left
R-modules.
(b) HomS(S,N)
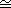 N, as left
S-modules. N, as left
S-modules.
10.6.9. Proposition. Let SUR be a bimodule. For
any modules RM and SN, there is an isomorphism
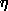 : HomS(
U : HomS(
U 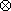 R
M , N) -> HomR( M, HomS (U,N) ). R
M , N) -> HomR( M, HomS (U,N) ).
10.6.10. Corollary. Let R and S be rings, and let
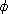 :R->S be a
ring homomorphism. Let M be any left R-module. Then S :R->S be a
ring homomorphism. Let M be any left R-module. Then S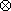 RM
is a left S-module, and for any left S-module N we have RM
is a left S-module, and for any left S-module N we have
HomS( S
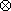 R
M, N) R
M, N) 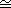 HomR(M,
N). HomR(M,
N).
Modules over a principal ideal domain
The fundamental theorem of finite abelian groups states that any finite abelian
group is isomorphic to a direct product of cyclic groups of prime power order.
From our current point of view, a finite abelian group is a module over the ring
of integers Z, and in this section we will show that we can
extend the fundamental theorem to modules over any principal ideal domain. This
includes the ring Q[x] of all polynomials with coefficients in
the field Q, and in this case all of the cyclic modules are
infinite, so we cannot restrict ourselves to finite modules. The appropriate
generalization is to consider finitely generated torsion modules, which we now
define. We will also consider finitely generated torsionfree modules, which turn
out to be free. In this section all rings will be commutative, and so we simply
refer to modules rather than left or right modules.
10.7.1. Definition. Let D be an integral domain, and let M be a
D-module.
An element m  M is called a torsion element if Ann(m)
M is called a torsion element if Ann(m)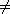 (0).
The set of all torsion elements of M is denoted by tor(M). (0).
The set of all torsion elements of M is denoted by tor(M).
If tor(M)=(0), then M is said to be a torsionfree module.
If tor(M) = M, then M is said to be a torsion module.
10.7.2. Proposition. Let D be an integral domain, and let M be a
D-module. Then tor(M) is a submodule of M, and M/tor(M) is a torsionfree module.
10.7.3. Lemma. Let D be a principal ideal domain with quotient field
Q. Then any nonzero finitely generated submodule of Q is free of rank 1.
10.7.4. Lemma. Let D be a principal ideal domain, and let M be a
finitely generated torsionfree D-module. If M contains a submodule N such that N
is free of rank 1 and M/N is a torsion module, then M is free of rank 1.
10.7.5. Theorem. If D is a principal ideal domain, then any nonzero
finitely generated torsionfree D-module is free.
10.7.6. Proposition. Let D be a principal ideal domain, and let M be a
finitely generated D-module. Then either M is torsion, or tor(M) has a
complement that is torsionfree. In the second case, M=tor(M) N
for a submodule N N
for a submodule N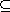 M
such that N is free of finite rank. M
such that N is free of finite rank.
The previous proposition shows that to complete the description of all
finitely generated modules over a principal ideal domain we only need to
characterize the finitely generated torsion modules. The first step is to show
that any finitely generated torsion module can be written as a direct sum of
finitely many indecomposable modules, and this is a consequence of the next
propositions.
10.7.7. Proposition. Let D be a principal ideal domain, and let a be a
nonzero element of D. If
a = p1m1 p2m2
. . . pkmk is the
decomposition of a into a product of irreducible elements, then we have the
following ring isomorphism.
D/aD
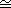 (D/p1m1D) (D/p1m1D)
 (D/p2m2D) (D/p2m2D)
 .
. . .
. .
 (D/pkmkD) (D/pkmkD)
10.7.8. Proposition. Let D be a principal ideal domain, let p be an
irreducible element of D, and let M be any indecomposable D-module with Ann(M)=pkD.
Then M is a cyclic module isomorphic to D/pkD.
10.7.9. Theorem. Let D be a principal ideal domain, and let M be a
finitely generated D-module. Then M is isomorphic to a finite direct sum of
cyclic submodules each isomorphic to either D or D/pkD, for some
irreducible element p of D. Moreover, the decomposition is unique up to the
order of the factors.
|

