Algebraic elements
6.1.1. Definition. The field F is said to be an extension field of
the field K if K is a subset of F which is a field under the operations of F.
6.1.2. Definition. Let F be an extension field of K and let u
 F. If there
exists a nonzero polynomial f(x) F. If there
exists a nonzero polynomial f(x)
 K[x] such
that f(u)=0, then u is said to be algebraic over K. If there does not
exist such a polynomial, then u is said to be transcendental over K. K[x] such
that f(u)=0, then u is said to be algebraic over K. If there does not
exist such a polynomial, then u is said to be transcendental over K.
6.1.3. Proposition. Let F be an extension field of K, and let u
 F be
algebraic over K. Then there exists a unique monic irreducible polynomial p(x) F be
algebraic over K. Then there exists a unique monic irreducible polynomial p(x)
 K[x] such
that p(u)=0. It is characterized as the monic polynomial of minimal degree that
has u as a root. K[x] such
that p(u)=0. It is characterized as the monic polynomial of minimal degree that
has u as a root.
Furthermore, if f(x) is any polynomial in K[x] with f(u)=0, then p(x) | f(x).
6.1.4. Definition. Let F be an extension field of K, and let u be an
algebraic element of F. The monic polynomial p(x) of minimal degree in K[x] such
that p(u)=0 is called the minimal polynomial of u over K. The degree of
the minimal polynomial of u over K is called the degree of u over K.
6.1.5. Definition. Let F be an extension field of K, and let u1,
u2, . . . , un
 F. The
smallest subfield of F that contains K and u1, u2, . . . ,
un will be denoted by F. The
smallest subfield of F that contains K and u1, u2, . . . ,
un will be denoted by
K ( u1, u2, . . . , un ).
It is called the extension field of K generated by u1, u2,
. . . , un .
If F = K(u) for a single element u F,
then F is said to be a simple extension of K. F,
then F is said to be a simple extension of K.
6.1.6. Proposition. Let F be an extension field of K, and let u
 F. F.
- (a) If u is algebraic over K, then K(u)
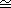 K[x]/<p(x)>, where p(x) is the minimal polynomial of u over K.
K[x]/<p(x)>, where p(x) is the minimal polynomial of u over K.
- (b) If u is transcendental over K, then K(u)
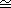 K(x),
where K(x) is the quotient field of the integral domain K[x]. K(x),
where K(x) is the quotient field of the integral domain K[x].
The next proposition is simply a restatement of
Kronecker's
theorem.
6.1.7. Proposition. Let K be a field and let p(x)
 K[x] be any
irreducible polynomial. Then there exists an extension field F of K and an
element u K[x] be any
irreducible polynomial. Then there exists an extension field F of K and an
element u  F
such that the minimal polynomial of u over K is p(x). F
such that the minimal polynomial of u over K is p(x).
Finite and algebraic extensions
6.2.1. Proposition. Let F be an extension field of K and let u
 F be an
element algebraic over K. If the minimal polynomial of u over K has degree n,
then K(u) is an n-dimensional vector space over K. F be an
element algebraic over K. If the minimal polynomial of u over K has degree n,
then K(u) is an n-dimensional vector space over K.
6.2.2. Definition. Let F be an extension field of K. If the dimension
of F as a vector space over K is finite, then F is said to be a finite
extension of K.
The dimension of F as a vector space over K is called the degree of F
over K, and is denoted by [F:K].
6.2.3. Proposition. Let F be an extension field of K and let u
 F. The
following conditions are equivalent: F. The
following conditions are equivalent:
- (1) u is algebraic over K;
- (2) K(u) is a finite extension of K;
- (3) u belongs to a finite extension of K.
6.2.4. Theorem. Let E be a finite extension of K and let F be a finite
extension of E. Then F is a finite extension of K, and
[F:K] = [F:E][E:K].
6.2.5. Corollary. Let F be a finite extension of K. Then the degree of
any element of F is a divisor of [F:K].
6.2.6 Corollary. Let F be an extension field of K, with algebraic
elements u1, u2, . . . , un
 F. Then the
degree of F. Then the
degree of
K ( u1, u2, . . . , un )
over K is at most the product of the degrees of ui over K, for 1
 i i
 n. n.
6.2.7. Corollary. Let F be an extension field of K. The set of all
elements of F that are algebraic over K forms a subfield of F.
6.2.8. Definition. An extension field F of K is said to be
algebraic over K if each element of F is algebraic over K.
6.2.9. Proposition. Every finite extension is an algebraic extension.
Example. 6.2.3. (Algebraic numbers) Let Q* be the set of all
complex numbers u
 C such
that u is algebraic over Q. Then Q* is a subfield of C by
Corollary 6.2.7, called the field of algebraic numbers. C such
that u is algebraic over Q. Then Q* is a subfield of C by
Corollary 6.2.7, called the field of algebraic numbers.
6.2.10. Proposition. Let F be an algebraic extension of E and let E be
an algebraic extension of K. Then F is an algebraic extension of K.
Geometric constructions
6.3.1. Definition. The real number a is said to be a constructible
number if it is possible to construct a line segment of length |a| by using
only a straightedge and compass.
6.3.2. Proposition. The set of all constructible real numbers is a
subfield of the field of all real numbers.
6.3.3. Definition. Let F be a subfield of R. The set of all
points (x,y) in the Euclidean plane R2 such that x,y
 F is called
the plane of F. F is called
the plane of F.
A straight line with an equation of the form ax+by+c = 0, for elements a,b,c
 F, is called
a line in F. F, is called
a line in F.
Any circle with an equation of the form x2 + y2 + ax + by
+ c = 0, for elements a,b,c
 F, is called
a circle in F. F, is called
a circle in F.
6.3.4. Lemma. Let F be a subfield of R.
- (a) Any straight line joining two points in the plane of F is a
line in F.
- (b) Any circle with its radius in F and its center in the plane
of F is a circle in F.
6.3.5. Lemma. The points of intersection of lines in F and circles in F
lie in the plane of F(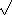 u),
for some u u),
for some u  F. F.
6.3.6. Theorem. The real number u is constructible if and only if
there exists a finite set u1, u2, . . . , un of
real numbers such that
- (i) u12
 Q, Q,
- (ii) ui2
 Q(u1,...,ui-1),
for i=2,..., and Q(u1,...,ui-1),
for i=2,..., and
- (iii) u
 Q(u1,...,un). Q(u1,...,un).
6.3.7. Corollary. If u is a constructible real number, then u is
algebraic over Q, and the degree of its minimal polynomial over Q
is a power of 2.
6.3.9. Theorem. It is impossible to find a general construction for
trisecting an angle, duplicating a cube, or squaring a circle.
Splitting fields
6.4.1. Definition. Let K be a field and let f(x) = a0 + a1
x + � � � + anxn be a polynomial in K[x] of degree n>0. An
extension field F of K is called a splitting field for f(x) over K if
there exist elements r1, r2, . . . , rn
 F such that F such that
- (i) f(x) = an (x-r1) (x-r2) �
� � (x-rn), and
- (ii) F = K(r1,r2,...,rn).
In the above situation we usually say that f(x) splits over the field F.
The elements r1, r2, . . . , rn are roots of
f(x), and so F is obtained by adjoining to K a complete set of roots of f(x).
6.4.2. Theorem. Let f(x)
 K[x] be a
polynomial of degree n>0. Then there exists a splitting field F for f(x) over K,
with [F:K] K[x] be a
polynomial of degree n>0. Then there exists a splitting field F for f(x) over K,
with [F:K]  n!.
n!.
6.4.3. Lemma. Let
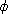 : K -> L be
an isomorphism of fields. Let F be an extension field of K such that F = K(u)
for an algebraic element u : K -> L be
an isomorphism of fields. Let F be an extension field of K such that F = K(u)
for an algebraic element u
 F. Let p(x)
be the minimal polynomial of u over K. If v is any root of the image q(x) of
p(x) under F. Let p(x)
be the minimal polynomial of u over K. If v is any root of the image q(x) of
p(x) under 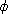 ,
and E=L(v), then there is a unique way to extend ,
and E=L(v), then there is a unique way to extend
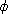 to an
isomorphism to an
isomorphism 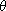 : F -> E such that
: F -> E such that
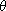 (u) = v and (u) = v and
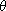 (a) = (a) =
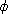 (a) for all a (a) for all a
 K. K.
6.4.5. Theorem. Let f(x) be a polynomial over the field K. The
splitting field of f(x) over K is unique up to isomorphism.
Finite fields
6.5.1. Proposition. Let F be a finite field of characteristic p. Then F
has pn elements, for some positive integer n.
If F is any field, then the smallest subfield of F that contains the identity
element 1 is called the prime subfield of F. If F is a finite field, then
its prime subfield is isomorphic to Zp, where p=chr(F) for
some prime p.
6.5.2. Theorem. Let F be a finite field with k = pn
elements. Then F is the splitting field of the polynomial xk-x over
the prime subfield of F.
Example 6.5.1. [Wilson's theorem] Let p > 2 be a prime number.
Then
(p-1)!
 -1 (mod
p). -1 (mod
p).
6.5.3. Corollary. Two finite fields are isomorphic if and only if they
have the same number of elements.
6.5.4. Lemma. Let F be a field of prime characteristic p, let n
 Z+,
and let k = pn. Then Z+,
and let k = pn. Then
{ a
 F | ak
= a } F | ak
= a }
is a subfield of F.
6.5.5. Proposition. Let F be a field with pn elements. Each
subfield of F has pm elements for some divisor m of n. Conversely,
for each positive divisor m of n there exists a unique subfield of F with pm
elements.
6.5.6. Lemma. Let F be a field of characteristic p. If n is a positive
integer not divisible by p, then the polynomial xn-1 has no repeated
roots in any extension field of F.
6.5.7. Theorem. For each prime p and each positive integer n, there
exists a field with pn elements.
6.5.8. Definition. Let p be a prime number and let n
 Z+.
The field (unique up to isomorphism) with pn elements is called the
Galois field of order pn, denoted by GF(pn). Z+.
The field (unique up to isomorphism) with pn elements is called the
Galois field of order pn, denoted by GF(pn).
6.5.9. Lemma. Let G be a finite abelian group. If a
 G is an
element of maximal order in G, then the order of every element of G is a divisor
of the order of a. G is an
element of maximal order in G, then the order of every element of G is a divisor
of the order of a.
6.5.10. Theorem. The multiplicative group of nonzero elements of a
finite field is cyclic.
6.5.11. Theorem. Any finite field is a simple extension of its prime
subfield.
6.5.12. Corollary. For each positive integer n there exists an
irreducible polynomial of degree n over GF(p).
Irreducible polynomials over finite fields
6.6.1. Theorem. Let F = GF(q), where q = pn, and let k = qm.
The irreducible factors of xk-x in F[x] are precisely the monic
irreducible polynomials in F[x] whose degree is a divisor of m.
Convention: In the notation
 d | n
and d | n
and  d
| n we will assume that d | n refers to the positive divisors of n. d
| n we will assume that d | n refers to the positive divisors of n.
6.6.2. Definition. If d is a positive integer, we define the
Moebius function
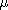 (d) as
follows: (d) as
follows:
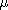 (1) =
1; (1) =
1;
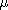 (d) =
1 if d has an even number of prime factors (each occurring only once); (d) =
1 if d has an even number of prime factors (each occurring only once);
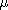 (d) =
-1 if d has an odd number of prime factors (each occurring only once); (d) =
-1 if d has an odd number of prime factors (each occurring only once);
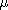 (d) =
0 if d is divisible by the square of a prime. (d) =
0 if d is divisible by the square of a prime.
6.6.3. Proposition. If m, n
 Z+
and gcd(m,n)=1, then Z+
and gcd(m,n)=1, then
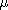 (mn) = (mn) =
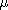 (m) (m)
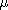 (n). (n).
If R is a commutative ring, then a function f : Z+ -> R
is said to be a multiplicative function if
f(mn) = f(m)f(n),
whenever gcd(m,n)=1.
6.6.4. Proposition. Let R be a commutative ring, and let f : Z+
-> R be a multiplicative function. If F : Z+ -> R is
defined by
F(n) =
 d | n
f(d), d | n
f(d),
for all n  Z+, then F is a multiplicative function.
Z+, then F is a multiplicative function.
6.6.5. Proposition. For any positive integer n,
 d | n d | n
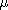 (d) = 1 if n
= 1, and (d) = 1 if n
= 1, and
 d | n d | n
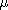 (d) = 0 if n
> 1. (d) = 0 if n
> 1.
6.6.6. Theorem. [Moebius Inversion Formula] Let R be a commutative ring,
and let f : Z+ -> R be any function. If the function F
: Z+ -> R is defined by
F(n) =
 d | n
f(d), for all n d | n
f(d), for all n
 Z+, Z+,
then
f(m) =
 n | m n | m
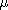 ( m/n ) F(n),
for all m ( m/n ) F(n),
for all m  Z+.
Z+.
6.6.7. Theorem. [Moebius Inversion Formula (2)] Let R be a commutative
ring, and let g : Z+ -> R be any function. If the
function G : Z+ -> R is defined by
G(n) =
 d |
n g(d), for all n d |
n g(d), for all n
 Z+, Z+,
then
g(m) =
 n |
m G(n)k, for all m n |
m G(n)k, for all m
 Z+, Z+,
where k = 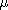 (
m/n ). (
m/n ).
6.6.8. Definition. The number of irreducible polynomials of degree m
over the finite field GF(q), where q is a prime power, will be denoted by Iq(m).
The following formula for Iq(m) is due to Gauss.
6.6.9. Theorem. For any prime power q and any positive integer m,
Iq(m) = (1/m)
 d | m d | m
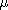 ( m / d ) qd. ( m / d ) qd.
6.6.10. Corollary. For all positive integers m and all prime powers q we
have Iq(m)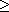 1. 1.
Quadratic reciprocity
6.7.1. Definition. Let n be a positive integer, and let a be an integer
such that n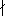 a.
Then a is called a quadratic residue modulo n if the congruence x2 a.
Then a is called a quadratic residue modulo n if the congruence x2 a(mod
n) is solvable, and a quadratic nonresidue otherwise. a(mod
n) is solvable, and a quadratic nonresidue otherwise.
When n is a prime, we write
 =1 if a is
a quadratic residue modulo n and =1 if a is
a quadratic residue modulo n and
 =-1 if a is
a quadratic nonresidue modulo n. The symbol =-1 if a is
a quadratic nonresidue modulo n. The symbol
 is called
the Legendre symbol. is called
the Legendre symbol.
6.7.2. Proposition. [Euler's Criterion] If p is an odd prime, and if a
 Z with
p Z with
p 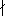 a, then a, then
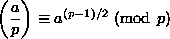
6.7.3. Theorem. [Quadratic Reciprocity] Let p, q be distinct odd primes.
Then
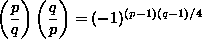
6.7.4. Theorem. Let p be an odd prime. Then
- (i)
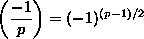 , and , and
- (ii)
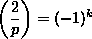 , where
k = (p2 - 1)/8. , where
k = (p2 - 1)/8.
|

