Functions and equivalence relations
2.1.1. Definition. Let S and T be sets. A function from S into T
is a subset F of S � T such that for each element x
 S there is
exactly one element y S there is
exactly one element y
 T such that
(x,y) T such that
(x,y)  F. The
set S is called the domain of the function, and the set T is called the
codomain of the function. F. The
set S is called the domain of the function, and the set T is called the
codomain of the function.
The subset { y  T | (x,y)
T | (x,y)  F
for some x F
for some x  S
} of the codomain is called the image of the function. S
} of the codomain is called the image of the function.
Example 2.1.1. Let S = { 1,2,3 } and T = { u,v,w }. The subsets
F1 = { (1,u), (2,v), (3,w) } and
F2 = { (1,u),(2,u),(3,u) }
of S � T both define functions since in both cases each element of S occurs
exactly once among the ordered pairs. The subset
F3 = { (1,u),(3,w) }
does not define a function with domain S because the element 2
 S does not
appear as the first component of any ordered pair. S does not
appear as the first component of any ordered pair.
Note that F3 is a function if the domain is changed to the set { 1,3
}.
Unlike the conventions used in calculus, the domain and codomain must be
specified as well as the ``rule of correspondence'' (list of pairs) when you are
presenting a function. The subset
F4 = { (1,u),(2,u),(2,v),(3,w) }
does not define a function since 2 appears as the first component of two ordered
pairs. When a candidate such as F4 fails to be a function in this
way, we say that it is not ``well-defined.''
2.1.2. Definition. Let f:S->T and g:T->U be functions. The
composition g � f of f and g is the function from S to U defined by the
formula (g � f)(x) = g(f(x)) for all x
 S. S.
2.1.3. Proposition. Composition of functions is associative.
2.1.4. Definition. Let f:S->T be a function. Then f is said to map S
onto T if for each element y
 T there
exists an element x T there
exists an element x
 S with f(x) =
y. S with f(x) =
y.
If f(x1) = f(x2) implies x1 = x2 for
all elements x1, x2
 S, then f is
said to be a one-to-one function. S, then f is
said to be a one-to-one function.
If f is both one-to-one and onto, then it is called a one-to-one
correspondence from S to T.
2.1.5. Proposition. Let f:S->T be a function. Suppose that S and T are
finite sets with the same number of elements. Then f is one-to-one if and only
if it is onto.
2.1.6. Proposition. Let f:S->T and g:T->U be functions.
- (a) If f and g are one-to-one, then g � f is one-to-one.
- (b) If f and g are onto, then g � f is onto.
2.1.7. Definition. Let S be a set. The identity function 1S:S->S
is defined by the formula
1S(x) = x for all x
 S. S.
If f:S->T is a function, then a function g:T->S is called an inverse for
f if
g � f = 1S and f � g = 1T.
2.1.8. Proposition. Let f:S->T be a function. If f has an inverse, then
it must be one-to-one and onto. Conversely, if f is one-to-one and onto, then it
has a unique inverse.
2.2.1. Definition. Let S be a set. A subset R of S � S is called an
equivalence relation on S if
- (i) for all a
 S, (a,a) S, (a,a)
 R; R;
- (ii) for all a,b
 S, if
(a,b) S, if
(a,b)  R
then (b,a) R
then (b,a)  R;
R;
- (iii) for all a,b,c
 S, if
(a,b) S, if
(a,b)  R
and (b,c) R
and (b,c)  R, then (a,c)
R, then (a,c)
 R. R.
We will write a
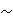 b to denote
the fact that (a,b) b to denote
the fact that (a,b)
 R. R.
2.2.2. Definition. Let
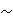 be an
equivalence relation on the set S. For a given element a be an
equivalence relation on the set S. For a given element a
 S, we define
the equivalence class of a to be the set of all elements of S that are
equivalent to a. S, we define
the equivalence class of a to be the set of all elements of S that are
equivalent to a.
We will use the notation [a]. In symbols,
[a] = { x
 S | x S | x
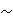 a }. a }.
The notation S/
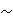 will be used
for the collection of all equivalence classes of S under will be used
for the collection of all equivalence classes of S under
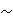 . .
Example. (S/f) 2.2.2. Let f:S->T be any function. For x1, x2
 S we define S we define
x1 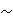 x2 if f(x1) = f(x2). Then for all x1,
x2, x3
x2 if f(x1) = f(x2). Then for all x1,
x2, x3
 S we have S we have
(i) f(x1) = f(x1);
(ii) if f(x1) = f(x2), then f(x2) = f(x1);
(iii) if f(x1) = f(x2) and f(x2) = f(x3),
then f(x1) = f(x3).
This shows that we have defined an equivalence relation on the set S. The proof
of this is easy because the equivalence relation is defined in terms of equality
of the images f(x), and equality is the most elementary equivalence relation.
The collection of all equivalence classes of S under
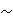 will be
denoted by S/f. will be
denoted by S/f.
2.2.3. Proposition. Let S be a set, and let
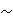 be an
equivalence relation on S. Then each element of S belongs to exactly one of the
equivalence classes of S determined by the relation be an
equivalence relation on S. Then each element of S belongs to exactly one of the
equivalence classes of S determined by the relation
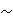 . .
2.2.4. Definition. Let S be any set. A family P of subsets of S is
called a partition of S if each element of S belongs to exactly one of
the members of P.
2.2.5. Proposition. Any partition P of a set S determines an
equivalence relation.
2.2.6. Theorem. If f:S->T is any function, and
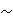 is the
equivalence relation defined on S by letting is the
equivalence relation defined on S by letting
x1 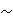 x2 if f(x1) = f(x2), for all x1, x2
x2 if f(x1) = f(x2), for all x1, x2
 S, then there
is a one-to-one correspondence between the elements of the image f(S) of S under
f and the equivalence classes S/f of the relation S, then there
is a one-to-one correspondence between the elements of the image f(S) of S under
f and the equivalence classes S/f of the relation
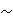 . .
If f:S ->T is a function and y belongs to the image f(S), then the inverse
image of y is
f -1(y) = { x
 S | f(x) = y
} . S | f(x) = y
} .
The inverse images of elements of f(S) are the equivalence classes in S/f. (Note
carefully that we are not implying that f has an inverse function.)
Permutations
2.3.1. Definition. Let S be a set. A function
 :S->S is
called a permutation of S if :S->S is
called a permutation of S if
 is
one-to-one and onto. is
one-to-one and onto.
The set of all permutations of S will be denoted by Sym(S).
The set of all permutations of the set { 1, 2, ..., n } will be denoted by Sn.
Proposition 2.1.6 shows that the composition of two permutations in Sym(S) is
again a permutation. It is obvious that the identity function on S is one-to-one
and onto. Proposition 2.1.8 shows that any permutation in Sym(S) has an inverse
function that is also one-to-one and onto. We can summarize these important
properties as follows:
- (i) If
 , ,

 Sym(S),
then Sym(S),
then 

 Sym(S); Sym(S);
- (ii) 1S
 Sym(S); Sym(S);
- (iii) if

 Sym(S),
then Sym(S),
then  -1
-1
 Sym(S). Sym(S).
2.3.2. Definition. Let S be a set, and let

 Sym(S). Then Sym(S). Then
 is called
a cycle of length k if there exist elements a1, a2,
..., ak is called
a cycle of length k if there exist elements a1, a2,
..., ak
 S such that S such that
 (a1)
= a2, (a1)
= a2,
 (a2)
= a3, . . . , (a2)
= a3, . . . ,
 (ak-1)
= ak, (ak-1)
= ak,
 (ak)
= a1, and (ak)
= a1, and
 (x)=x for
all other elements x (x)=x for
all other elements x
 S with x S with x
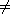 ai
for i = 1, 2, ..., k. ai
for i = 1, 2, ..., k.
In this case we write
 = (a1,a2,...,ak). = (a1,a2,...,ak).
We can also write
 = (a2,a3,...,ak,a1)
or = (a2,a3,...,ak,a1)
or  = (a3,...,ak,a1,a2),
etc. The notation for a cycle of length k can thus be written in k different
ways, depending on the starting point. The notation (1) is used for the identity
permutation. = (a3,...,ak,a1,a2),
etc. The notation for a cycle of length k can thus be written in k different
ways, depending on the starting point. The notation (1) is used for the identity
permutation.
2.3.3. Definition. Let
 = (a1,a2,...,ak)
and = (a1,a2,...,ak)
and  = (b1,b2,...,bm)
be cycles in Sym(S), for a set S. Then = (b1,b2,...,bm)
be cycles in Sym(S), for a set S. Then
 and and
 are said to
be disjoint if ai are said to
be disjoint if ai
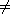 bj
for all i,j. bj
for all i,j.
2.3.4. Proposition. Let S be any set. If
 and and
 are disjoint
cycles in Sym(S), then are disjoint
cycles in Sym(S), then

 = =

 . .
2.3.5. Theorem. Every permutation in Sn can be written as a
product of disjoint cycles. The cycles that appear in the product are unique.
2.3.6. Definition. Let

 Sn.
The least positive integer m such that Sn.
The least positive integer m such that
 m
= (1) is called the order of m
= (1) is called the order of
 . .
2.3.7. Proposition. Let

 Sn
have order m. Then for all integers j,k we have Sn
have order m. Then for all integers j,k we have
 j
= j
=  k
if and only if j k
if and only if j
 k (mod m). k (mod m).
2.3.8. Proposition. Let

 Sn
be written as a product of disjoint cycles. Then the order of Sn
be written as a product of disjoint cycles. Then the order of
 is the
least common multiple of the lengths of its cycles. is the
least common multiple of the lengths of its cycles.
2.3.9. Definition. A cycle (a1,a2) of length two
is called a transposition.
2.3.10 Proposition. Any permutation in Sn, where n
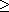 2, can be
written as a product of transpositions. 2, can be
written as a product of transpositions.
2.3.11. Theorem. If a permutation is written as a product of
transpositions in two ways, then the number of transpositions is either even in
both cases or odd in both cases.
2.3.12. Definition. A permutation
 is called
even if it can be written as a product of an even number of
transpositions, and odd if it can be written as a product of an odd
number of transpositions. is called
even if it can be written as a product of an even number of
transpositions, and odd if it can be written as a product of an odd
number of transpositions.
|

