Groups, in general
3.1.3. Definition. A group (G,�) is a nonempty set G
together with a binary operation � on G such that the following
conditions hold:
- (i) Closure: For all a,b
 G the
element a � b is a uniquely defined element of G. G the
element a � b is a uniquely defined element of G.
- (ii) Associativity: For all a,b,c
 G, we
have G, we
have
a � (b � c) = (a � b) � c.
- (iii) Identity: There exists an identity element
e
 G such
that G such
that
e � a = a and a � e = a
for all a  G.
G.
- (iv) Inverses: For each a
 G there
exists an inverse element a-1 G there
exists an inverse element a-1
 G such
that G such
that
a � a-1 = e and a-1 �
a = e.
We will usually simply write ab for the product a � b.
3.1.6. Proposition. (Cancellation Property for Groups) Let G be a
group, and let a,b,c
 G. G.
- (a) If ab=ac, then b=c.
- (b) If ac=bc, then a=b.
3.1.8. Definition. A group G is said to be abelian if ab=ba for
all a,b  G. G.
3.1.9. Definition. A group G is said to be a finite group if
the set G has a finite number of elements. In this case, the number of elements
is called the order of G, denoted by |G|.
3.2.7. Definition. Let a be an element of the group G. If there exists
a positive integer n such that an = e, then a is said to have
finite order, and the smallest such positive integer is called the order
of a, denoted by o(a).
If there does not exist a positive integer n such that an = e, then a
is said to have infinite order.
3.2.1. Definition. Let G be a group, and let H be a subset of G. Then
H is called a subgroup of G if H is itself a group, under the operation
induced by G.
3.2.2. Proposition. Let G be a group with identity element e, and let
H be a subset of G. Then H is a subgroup of G if and only if the following
conditions hold:
- (i) ab
 H for all
a,b H for all
a,b  H; H;
- (ii) e
 H; H;
- (iii) a-1
 H for all
a H for all
a  H. H.
3.2.10. Theorem. (Lagrange) If H is a subgroup of the finite group G,
then the order of H is a divisor of the order of G.
3.2.11. Corollary. Let G be a finite group of order n.
- (a) For any a
 G, o(a)
is a divisor of n. G, o(a)
is a divisor of n.
- (b) For any a
 G, an
= e. G, an
= e.
Example 3.2.12.
(Euler's
theorem) Let G be the multiplicative group of congruence classes modulo n.
The order of G is given by
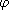 (n), and
so by Corollary 3.2.11, raising any congruence class to the power (n), and
so by Corollary 3.2.11, raising any congruence class to the power
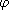 (n) must
give the identity element. (n) must
give the identity element.
3.2.12. Corollary. Any group of prime order is cyclic.
3.4.1. Definition. Let G1 and G2 be groups, and
let 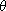 : G1
-> G2 be a function. Then : G1
-> G2 be a function. Then
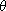 is said to
be a group isomorphism if is said to
be a group isomorphism if
- (i)
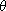 is
one-to-one and onto and is
one-to-one and onto and
- (ii)
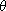 (ab) = (ab) =
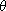 (a) (a)
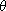 (b) for
all a,b (b) for
all a,b  G1. G1.
In this case, G1 is said to be isomorphic to G2,
and this is denoted by G1
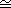 G2. G2.
3.4.3. Proposition. Let
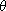 : G1
-> G2 be an isomorphism of groups. : G1
-> G2 be an isomorphism of groups.
- (a) If a has order n in G1, then
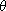 (a) has
order n in G2. (a) has
order n in G2.
- (b) If G1 is abelian, then so is G2.
- (c) If G1 is cyclic, then so is G2.
Cyclic groups
3.2.5 Definition. Let G be a group, and let a be any element of G. The
set
<a> = { x
 G | x = an
for some n G | x = an
for some n  Z
} Z
}
is called the cyclic subgroup generated by a.
The group G is called a cyclic group if there exists an element a
 G such that
G=<a>. In this case a is called a generator of G. G such that
G=<a>. In this case a is called a generator of G.
3.2.6 Proposition. Let G be a group, and let a
 G. G.
- (a) The set <a> is a subgroup of G.
- (b) If K is any subgroup of G such that a
 K, then
<a> K, then
<a> 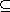 K.
K.
3.2.8. Proposition. Let a be an element of the group G.
- (a) If a has infinite order, and ak = am
for integers k,m, them k=m.
- (b) If a has finite order and k is any integer, then ak
= e if and only if o(a) | k.
- (c) If a has finite order o(a)=n, then for all integers k, m, we
have
ak = am if and only if k
 m (mod
n). m (mod
n).
Furthermore, |<a>|=o(a).
Corollaries to Lagrange's Theorem (restated):
- (a) For any a
 G, o(a)
is a divisor of |G|. G, o(a)
is a divisor of |G|.
- (b) For any a
 G, an
= e, for n = |G|. G, an
= e, for n = |G|.
- (c) Any group of prime order is cyclic.
3.5.1. Theorem. Every subgroup of a cyclic group is cyclic.
3.5.2 Theorem. Let G cyclic group.
- (a) If G is infinite, then G
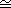 Z. Z.
- (b) If |G| = n, then G
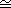 Zn. Zn.
3.5.3. Proposition. Let G = <a> be a cyclic group with |G| = n.
- (a) If m
 Z,
then <am> = <ad>, where d=gcd(m,n), and am
has order n/d. Z,
then <am> = <ad>, where d=gcd(m,n), and am
has order n/d.
- (b) The element ak generates G if and only if
gcd(k,n)=1.
(c) The subgroups of G are in one-to-one correspondence with the
positive divisors of n.
(d) If m and k are divisors of n, then <am>
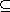 <ak>
if and only if k | m. <ak>
if and only if k | m.
3.5.6. Definition. Let G be a group. If there exists a positive integer N
such that aN=e for all a
 G, then the
smallest such positive integer is called the exponent of G. G, then the
smallest such positive integer is called the exponent of G.
3.5.7. Lemma. Let G be a group, and let a,b
 G be elements
such that ab = ba. If the orders of a and b are relatively prime, then o(ab) =
o(a)o(b). G be elements
such that ab = ba. If the orders of a and b are relatively prime, then o(ab) =
o(a)o(b).
3.5.8. Proposition. Let G be a finite abelian group.
- (a) The exponent of G is equal to the order of any element of G
of maximal order.
- (b) The group G is cyclic if and only if its exponent is equal to
its order.
Permutation groups
3.1.4. Definition. The set of all permutations of a set S is denoted by
Sym(S).
The set of all permutations of the set {1,2,...,n} is denoted by Sn.
3.1.5. Proposition. If S is any nonempty set, then Sym(S) is a group
under the operation of composition of functions.
2.3.5. Theorem. Every permutation in Sn can be written as a
product of disjoint cycles. The cycles that appear in the product are unique.
2.3.8 Proposition. If a permutation in Sn is written as a
product of disjoint cycles, then its order is the least common multiple of the
lengths of its cycles.
3.6.1. Definition. Any subgroup of the symmetric group Sym(S)
on a set S is called a permutation group or group of permutations.
3.6.2. Theorem. (Cayley) Every group is isomorphic to a permutation
group.
3.6.3. Definition. Let n > 2 be an integer. The group of rigid motions
of a regular n-gon is called the nth dihedral group, denoted by
Dn.
We can describe the nth dihedral group as
Dn= { ak, akb | 0
 k < n }, k < n },
subject to the relations o(a) = n, o(b) = 2, and ba = a-1b.
2.3.11. Theorem. If a permutation is written as a product of
transpositions in two ways, then the number of transpositions is either even in
both cases or odd in both cases.
2.3.12. Definition. A permutation is called even if it can be
written as a product of an even number of transpositions, and odd if it
can be written as a product of an odd number of transpositions.
3.6.4. Proposition. The set of all even permutations of Sn
is a subgroup of Sn.
3.6.5. Definition. The set of all even permutations of Sn
is called the alternating group on n elements, and will be denoted by An.
Other examples
Example 3.1.4. (Group of units modulo n) Let n be a positive integer. The
set of units modulo n, denoted by Zn�, is an
abelian group under multiplication of congruence classes. Its order is given by
the value 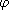 (n)
of Euler's
phi-function. (n)
of Euler's
phi-function.
3.1.10. Definition. The set of all invertible n � n matrices with
entries in R is called the general linear group of degree n over
the real numbers, and is denoted by GLn(R).
3.1.11. Proposition. The set GLn(R) forms a group
under matrix multiplication.
3.3.3. Definition. Let G1 and G2 be groups. The
set of all ordered pairs (x1,x2) such that x1
 G1
and x2 G1
and x2
 G2
is called the direct product of G1 and G2, denoted
by G1 � G2. G2
is called the direct product of G1 and G2, denoted
by G1 � G2.
3.3.4. Proposition. Let G1 and G2 be groups.
- (a) The direct product G1 � G2 is a group
under the multiplication defined for all
(a1,a2), (b1,b2)
 G1
� G2 by G1
� G2 by
(a1,a2) (b1,b2)
= (a1b1,a2b2).
- (b) If the elements a1
 G1
and a2 G1
and a2
 G2
have orders n and m, respectively, then in G2
have orders n and m, respectively, then in
G1 � G2 the element (a1,a2) has
order lcm[n,m].
3.3.5. Definition. Let F be a set with two binary operations + and �
with respective identity elements 0 and 1, where 1 is distinct from 0. Then F is
called a field if
- (i) the set of all elements of F is an abelian group under +;
- (ii) the set of all nonzero elements of F is an abelian group
under �;
- (iii) a � (b+c) = a � b + a � c for all
a,b,c in F.
3.3.6. Definition. Let F be a field. The set of all invertible n � n
matrices with entries in F is called the general linear group of degree n
over F, and is denoted by GLn(F).
3.3.7. Proposition. Let F be a field. Then GLn(F) is a
group under matrix multiplication.
3.4.5. Proposition. If m,n are positive integers such that gcd(m,n)=1,
then
Zm � Zn
 Zmn. Zmn.
Example. 3.3.7. (Quaternion group)
Consider the following set of invertible 2 � 2 matrices with entries in the
field of complex numbers.
�
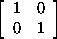 ,
� ,
�
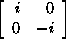 ,
� ,
�
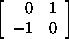 ,
� ,
�
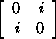 . .
If we let
1 =
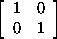 ,
i = ,
i =
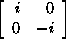 ,
j = ,
j =
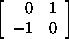 ,
k = ,
k =
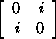
then we have the identities
i2 = j2 = k2
= -1;
ij = k, jk = i, ki = j;
ji = -k, kj = -i, ik = -j.
These elements form a nonabelian group Q of order 8 called the quaternion
group, or group of quaternion units.
|

