Prime and primitive ideals
11.1.1. Definition. A proper
ideal P of
the ring R
is called a prime ideal if AB
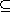 P implies A
P implies A
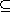 P or B
P or B
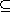 P, for any ideals A, B of R.
P, for any ideals A, B of R.
A proper ideal I of the ring R is called a semiprime ideal if it is an
intersection of prime ideals of R.
A proper ideal P of the ring R is called a left primitive ideal if it is
the annihilator of a simple left R-module.
11.1.2. Definition. The ring R is called a simple ring if (0)
is a maximal ideal; it is called a prime ring if (0) is a prime ideal,
and a semiprime ring if (0) is a semiprime ideal. Finally, R is said to
be a (left) primitive ring if (0) is a primitive ideal.
11.1.3. Proposition. The following conditions are equivalent for the
proper ideal P of the ring R:
(1) P is a prime ideal;
(2) AB
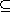 P implies A
P implies A
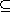 P or B
P or B
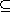 P, for any ideals A, B of R which contain P;
P, for any ideals A, B of R which contain P;
(3) AB
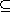 P implies A = P or B = P, for any left ideals A, B of R with P
P implies A = P or B = P, for any left ideals A, B of R with P
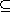 A and P
A and P
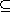 B;
B;
(4) aRb
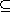 P implies a
P implies a
 P or b P or b
 P, for
any a,b P, for
any a,b  R. R.
11.1.4. Definition. The nonzero module RM is called a
prime module if AN = (0) implies N = (0) or AM = (0), for any ideal A of R
and any submodule N of M.
11.1.5. Proposition. The annihilator of a prime module is a prime
ideal.
11.1.6. Proposition. Any maximal ideal is primitive, and any primitive
ideal is prime.
In a left
Artinian ring, the notions of maximal ideal, primitive ideal, and prime
ideal coincide.
An ideal I of the ring R is said to be nilpotent if An =
(0) for some positive integer n. It is said to be a nil ideal if for each
a  I there
exists a positive integer n such that an = 0. I there
exists a positive integer n such that an = 0.
11.1.7. Proposition. The following conditions are equivalent for the
proper ideal I of the ring R:
(1) I is a semiprime ideal;
(2) the ring R/I has no nonzero nilpotent ideals;
(3) AB
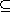 I implies A
I implies A B B
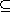 I, for any ideals A, B of R;
I, for any ideals A, B of R;
(4) AB
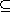 I implies A
I implies A B
= I, for any left ideals A, B of R with I B
= I, for any left ideals A, B of R with I
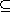 A and I
A and I
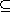 B;
B;
(5) aRa
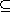 I implies a
I implies a
 I, for
all a I, for
all a  R. R.
11.1.8. Definition. Let RM be a left R-module. The
bicommutator of M is the subring of EndZ(M) defined by
BicR(M) = {
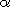
 EndZ(M)
| f EndZ(M)
| f 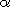 = =
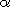 f
for all f f
for all f  EndR(M) }.
EndR(M) }.
11.1.9. Lemma. If M is any left R-module, then R/Ann(M) is isomorphic to
a subring of BicR(M).
11.1.10. Proposition. If P is a primitive ideal of the ring R, then
there exists a
division ring D and a vector space V over D for which R/P is isomorphic to a
subring of the ring of all linear transformations from V into V.
11.1.11. Proposition. Let M be a left R-module.
(a) The endomorphism ring EndR(Mn) is isomorphic to
the ring of n�n matrices with entries in EndR(M).
(b) The bicommutator BicR(Mn) is isomorphic to BicR(M).
The Jacobson radical
11.2.1. Definition. Let M be a left R-module. The intersection of all
maximal submodules of M is called the Jacobson radical of M, and is
denoted by J(M).
11.2.2. Definition. Let M be a left R-module.
The submodule N of M is called essential or large in M if N K K
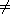 (0) for all nonzero submodules K of M.
(0) for all nonzero submodules K of M.
The submodule N is called superfluous or small in M if N+K
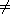 M for all proper submodules K of M.
M for all proper submodules K of M.
11.2.3. Proposition. Let N be a submodule of RM. If K is
maximal in the set of all submodules of M that have trivial intersection with N,
then N+K is essential in M, and (N+K)/K is essential in M/K.
11.2.4. Proposition. The
socle of
any module is the intersection of its essential submodules.
11.2.5. Definition. A radical for the class of left R-modules
is a function that assigns to each module RM a submodule
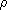 (M) such
that (M) such
that
(i) f(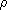 (M)) (M))
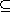
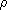 (N), for
all modules RN and all f (N), for
all modules RN and all f
 HomR(M,N); HomR(M,N);
(ii)
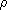 (M/ (M/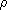 (M))
= (0). (M))
= (0).
11.2.6. Definition. Let C be any class of left R-modules. For any
module RM we make the following definition.
radC(M) =
 ker(f),
ker(f),
where the intersection is taken over all R-homomorphisms f : M -> X, for all X
in C.
11.2.7. Proposition. Let
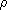 be a
radical for the class of left R-modules, and let F be the class of left
R-modules X for which be a
radical for the class of left R-modules, and let F be the class of left
R-modules X for which
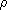 (X) = (0). (X) = (0).
(a) 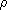 (R)
is a two-sided ideal of R. (R)
is a two-sided ideal of R.
(b) 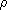 (R)
M (R)
M
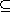
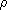 (M) for
all modules RM. (M) for
all modules RM.
(c) radF is a radical, and
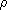 = radF. = radF.
(d) 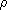 (R) =
(R) =
 Ann(X), where the intersection is taken over all modules X in F.
Ann(X), where the intersection is taken over all modules X in F.
11.2.8. Lemma. [Nakayama] If R M is finitely generated and
J(R)M = M, then M = (0).
11.2.9. Proposition. Let M be a left R-module.
(a) J(M) = { m
 M | Rm is
small in M }. M | Rm is
small in M }.
(b) J(M) is the sum of all small submodules of M.
(c) If M is finitely generated, then J(M) is a small submodule.
(d) If M is finitely generated, then M/J(M) is
semisimple if and only if it is Artinian.
11.2.10. Theorem. The Jacobson radical J(R) of the ring R is equal to
each of the following sets:
(1) The intersection of all maximal left ideals of R;
(2) The intersection of all maximal right ideals of R;
(3) The intersection of all left-primitive ideals of R;
(4) The intersection of all right-primitive ideals of R;
(5) { x
 R | 1-ax is
left invertible for all a R | 1-ax is
left invertible for all a
 R }; R };
(6) { x
 R | 1-xa is
right invertible for all a R | 1-xa is
right invertible for all a
 R }; R };
(7) The largest ideal J of R such that 1-x is invertible in R for all x
 J. J.
11.2.11. Definition. The ring R is said to be semiprimitive if
J(R) = (0).
11.2.12. Proposition. Let R be any ring.
(a) The Jacobson radical of R contains every nil ideal of R.
(b) If R is left Artinian, then the Jacobson radical of R is nilpotent.
Semisimple Artinian rings
11.3.1. Theorem. Any simple ring with a minimal left ideal is isomorphic
to a ring of n�n matrices over a division ring.
11.3.2. Theorem. [Artin-Wedderburn] The following conditions are
equivalent for a ring R with identity.
(1) R is left Artinian and J(R) = (0);
(2) RR is a semisimple module;
(3) R is isomorphic to a finite direct product of rings of n�n matrices
over division rings.
11.3.3. Definition. A ring which satisfies the conditions of the
previous theorem is said to be semisimple Artinian.
11.3.4. Corollary. The following conditions are equivalent for a ring
R with identity.
(1) R is semisimple Artinian;
(2) R is left Artinian and semiprime;
(3) every left R-module is
completely
reducible;
(4) every left R-module is
projective;
(5) every left R-module is
injective.
11.3.5. Theorem. [Hopkins] Any left Artinian ring is left Noetherian.
11.3.6. Lemma. Let RM be a simple module, and let D = EndR(M).
If DV is any finite dimensional subspace of DM, then
V = { m
 M | AnnR(V)
m = 0 }. M | AnnR(V)
m = 0 }.
Let V be a left vector space over a division ring D. A subring R is called a
dense subring of EndD(V) if for each n>0, each linearly
independent subset {u1,u2,...,un} of V, and
each arbitrary subset {v1,v2,...,vn} of V,
there exists an element
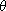
 R such that R such that
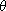 (ui)
= vi for all i = 1,...,n. (ui)
= vi for all i = 1,...,n.
11.3.7. Theorem. [Jacobson Density Theorem] Any (left) primitive ring
is isomorphic to a dense ring of linear transformations of a vector space over a
division ring.
11.3.8. Proposition. If RM is completely reducible and
finitely generated, then EndR(M) is isomorphic to a finite direct
product of rings of n�n matrices over division rings.
11.3.9. Definition. A ring R is called von Neumann regular if
for each a  R there exists b
R there exists b
 R such that
aba = a. R such that
aba = a.
11.3.10. Proposition. If RM is completely reducible, then
EndR(M) is von Neumann regular.
11.3.11. Proposition. The following conditions are equivalent for a
ring R.
(1) R is von Neumann regular;
(2) each
principal left ideal of R is generated by an
idempotent
element;
(3) each finitely generated left ideal of R is generated by an idempotent
element.
11.1.12. Proposition. If R is a von Neumann regular ring, then J(R) =
(0).
|

