Isomorphism theorems; automorphisms
7.1.1. Theorem. [First Isomorphism Theorem] Let G be a group with normal
subgroups N and H such that N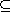 H.
Then H/N is a normal subgroup of G/N, and H.
Then H/N is a normal subgroup of G/N, and
(G / N) / (H / N)
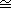 G / H. G / H.
7.1.2. Theorem. [Second Isomorphism Theorem] Let G be a group, let N be a
normal subgroup of G, and let H be any subgroup of G. Then HN is a subgroup of
G, H N is a
normal subgroup of H, and N is a
normal subgroup of H, and
(HN) / N
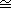 H / (H H / (H
 N). N).
7.1.3. Theorem. Let G be a group with normal subgroups H, K such that
HK=G and H K={e}.
Then K={e}.
Then
G
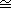 H � K
. H � K
.
7.1.4. Proposition. Let G be a group and let a
 G. The
function ia : G -> G defined by ia(x) = axa-1
for all x G. The
function ia : G -> G defined by ia(x) = axa-1
for all x  G
is an isomorphism. G
is an isomorphism.
7.1.5. Definition. Let G be a group. An isomorphism from G onto G is
called an automorphism of G. An automorphism of G of the form ia,
for some a  G,
where ia (x) = axa-1 for all x G,
where ia (x) = axa-1 for all x
 G, is called
an inner automorphism of G. The set of all automorphisms of G will be
denoted by Aut(G) and the set of all inner automorphisms of G will be denoted by
Inn(G). G, is called
an inner automorphism of G. The set of all automorphisms of G will be
denoted by Aut(G) and the set of all inner automorphisms of G will be denoted by
Inn(G).
7.1.6. Proposition. Let G be a group. Then Aut(G) is a group under
composition of functions, and Inn(G) is a normal subgroup of Aut(G).
7.1.7. Definition. For any group G, the subset
Z(G) = { x
 G | xg = gx
for all g G | xg = gx
for all g  G } G }
is called the center of G.
7.1.8. Proposition. For any group G, we have Inn(G)
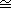 G/Z(G). G/Z(G).
Example. 7.1.1. Aut(Z)
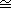 Z2
and Inn(Z) = {e} Z2
and Inn(Z) = {e}
Example. 7.1.2. Aut(Zn)
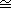 Zn� Zn�
Conjugacy
7.2.1. Definition. Let G be a group, and let x,y
 G. The
element y is said to be a conjugate of the element x if there exists an
element a G. The
element y is said to be a conjugate of the element x if there exists an
element a  G
such that y = axa-1. G
such that y = axa-1.
If H and K are subgroups of G, then K is said to be a conjugate subgroup of H
if there exists a
 G such that K
= aHa-1. G such that K
= aHa-1.
7.2.2. Proposition.
- (a) Conjugacy of elements defines an equivalence relation on any
group G.
- (b) Conjugacy of subgroups defines an equivalence relation on the
set of all subgroups of G.
7.2.3. Definition. Let G be a group. For any element x
 G, the set G, the set
{ a
 G | axa-1
= x } G | axa-1
= x }
is called the centralizer of x in G, denoted by C(x).
For any subgroup H of G, the set
{ a
 G | aHa-1
= H } G | aHa-1
= H }
is called the normalizer of H in G, denoted by N(H).
7.2.4. Proposition. Let G be a group and let x
 G. Then C(x)
is a subgroup of G. G. Then C(x)
is a subgroup of G.
7.2.5. Proposition. Let x be an element of the group G. Then the
elements of the conjugacy class of x are in one-to-one correspondence with the
left cosets of the centralizer C(x) of x in G.
Example. 7.2.3. Two permutations are conjugate in Sn if and
only if they have the same shape (i.e., the same number of disjoint cycles, of
the same lengths). Thus, in particular, cycles of the same length are always
conjugate.
7.2.6. Theorem. [Conjugacy class Equation] Let G be a finite group.
Then
| G | = | Z(G) | +
 [ G : C(x) ] [ G : C(x) ]
where the sum ranges over one element x from each nontrivial conjugacy class.
7.2.7. Definition. A group of order pn, with p a prime
number and n 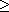 1, is called a p-group.
1, is called a p-group.
7.2.8. Theorem. [Burnside] Let p be a prime number. The center of any
p-group is nontrivial.
7.2.9. Corollary. Any group of order p2 (where p is prime)
is abelian.
7.2.10. Theorem. [Cauchy] If G is a finite group and p is a prime
divisor of the order of G, then G contains an element of order p.
Groups acting on sets
7.3.1. Definition. Let G be a group and let S be a set. A multiplication
of elements of S by elements of G (defined by a function from G � S -> S) is
called a group action of G on S provided for each x
 S: S:
- (i) a(bx) = (ab)x for all a,b
 G, and G, and
- (ii) ex = x for the identity element e of G.
7.3.2. Proposition. Let G be a group and let S be a set. Any group
homomorphism from G into the group Sym(S) of all permutations of S defines an
action of G on S. Conversely, every action of G on S arises in this way.
7.3.3. Definition. Let G be a group acting on the set S. For each
element x  S,
the set S,
the set
Gx = { s
 S | s=ax for
some a S | s=ax for
some a  G } G }
is called the orbit of x under G, and the set
Gx = { a
 G | ax = x } G | ax = x }
is called the stabilizer of x in G. The set
SG = { x
 S | ax = x
for all a S | ax = x
for all a  G } G }
is called the subset of S fixed by G.
7.3.4. Proposition. Let G be a group that acts on the set S, and let x S. S.
- (a) The stabilizer Gx of x in G is a subgroup of G.
- (b) There is a one-to-one correspondence between the elements of
the orbit Gx of x under G and the left cosets of Gx in G.
7.3.5. Proposition. Let G be a finite group acting on the set S.
- (a) The orbits of S (under the action of G) partition S.
- (b) For any x
 S, | Gx |
= [ G : Gx ]. S, | Gx |
= [ G : Gx ].
7.3.6. Theorem. Let G be a finite group acting on the finite set S.
Then
| S | = | SG | +

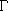 [ G
: Gx ], [ G
: Gx ],
where 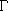 is a
set of representatives of the orbits Gx for which | Gx | > 1. is a
set of representatives of the orbits Gx for which | Gx | > 1.
7.3.7. Lemma. Let G be a finite p-group acting on the finite set S.
Then
| S |
 | SG
| (mod p). | SG
| (mod p).
7.3.8. Theorem. [Cauchy] If G is a finite group and p is a prime
divisor of |G|, then the number of solutions in G of the equation xp
= e is a multiple of p. In particular, G has an element of order p.
The Sylow theorems
7.4.1. Theorem. [First Sylow Theorem] Let G be a finite group. If p is a
prime such that pk is a divisor of |G| for some k
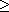 0, then G
contains a subgroup of order pk. 0, then G
contains a subgroup of order pk.
7.4.2. Definition. Let G be a finite group, and let p be a prime
number. A subgroup P of G is called a Sylow p-subgroup of G if |P| = pk
for some integer k
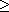 1 such that
pk is a divisor of |G| but pk+1 is not. 1 such that
pk is a divisor of |G| but pk+1 is not.
7.4.3. Lemma. Let G be a finite group with |G| = mpk, where
k 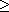 1 and m is
not divisible by p. If P is a normal Sylow p-subgroup, then P contains every
p-subgroup of G. 1 and m is
not divisible by p. If P is a normal Sylow p-subgroup, then P contains every
p-subgroup of G.
7.4.4. Theorem. [Second and Third Sylow Theorems] Let G be a finite
group of order n, and let p be a prime number.
- (a) All Sylow p-subgroups of G are conjugate, and any p-subgroup
of G is contained in a Sylow p-subgroup.
- (b) Let n = mpk, with gcd(m,p)=1, and let s be the
number of Sylow p-subgroups of G.
Then s | m and s
 1 (mod
p). 1 (mod
p).
7.4.5. Proposition. Let p > 2 be a prime, and let G be a group of
order 2p. Then G is either cyclic or isomorphic to the dihedral group Dp
of order 2p.
7.4.6. Proposition. Let G be a group of order pq, where p > q are
primes.
- (a) If q is not a divisor of p-1, then G is cyclic.
- (b) If q is a divisor of p-1, then either G is cyclic or else G
is generated by two elements a and b satisfying the following equations:
ap = e, bq = e, ba = anb
where n
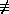 1
(mod p) but nq 1
(mod p) but nq
 1 (mod
p). 1 (mod
p).
Finite abelian groups
7.5.1. Theorem. A finite abelian group can be expressed as a direct
product of its Sylow p-subgroups.
7.5.2. Lemma. Let G be a finite abelian p-group, let a
 G be an
element of maximal order, and let b<a> be any coset of G/<a>. Then there exists
d G be an
element of maximal order, and let b<a> be any coset of G/<a>. Then there exists
d  G such that
d<a> = b<a> and <a> G such that
d<a> = b<a> and <a>
 <d> = {e}. <d> = {e}.
7.5.3. Lemma. Let G be a finite abelian p-group. If <a> is a cyclic
subgroup of G of maximal order, then there exists a subgroup H with G
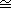 <a> � H. <a> � H.
7.5.4. Theorem. [Fundamental Theorem of Finite Abelian Groups] Any
finite abelian group is isomorphic to a direct product of cyclic groups of prime
power order. Any two such decompositions have the same number of factors of each
order.
7.5.5. Proposition. Let G be a finite abelian group. Then G is
isomorphic to a direct product of cyclic groups
Zn1 � Zn2
� � � � � Znk
such that ni | ni-1 for i = 2,3, . . . ,k.
7.5.6. Corollary. Let G be a finite abelian group. If a
 G is an
element of maximal order in G, then the order of every element of G is a divisor
of the order of a. G is an
element of maximal order in G, then the order of every element of G is a divisor
of the order of a.
7.5.8 Theorem. Let p be an odd prime, let k be a positive integer, and
let n = pk. Then Zn� is a cyclic group.
7.5.10. Theorem. If k
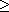 3, and n = 2k,
then Zn� is isomorphic to the direct product of a
cyclic group of order 2 and a cyclic group of order 2k-2. 3, and n = 2k,
then Zn� is isomorphic to the direct product of a
cyclic group of order 2 and a cyclic group of order 2k-2.
7.5.11. Corollary. The group Zn� is
cyclic if and only if n is of the form 2, 4, pk, or 2pk
for an odd prime p.
In elementary number theory, an integer g is called a primitive root
for the modulus n if Zn� is a cyclic group and [g]n
is a generator for Zn�. Corollary 7.5.11 determines
which moduli n have primitive roots. The proof of Theorem 7.5.8 shows how to
find a generator for Zn�, where n = pk.
Solvable groups
7.6.1. Definition. The group G is said to be solvable if there
exists a finite chain of subgroups
G = N0
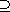 N1 N1
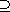 � �
� � �
� 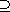 Nn
such that Nn
such that
- (i) Ni is a normal subgroup in Ni-1 for i =
1,2, . . . ,n,
- (ii) Ni-1 / Ni is abelian for i = 1,2, . .
. ,n, and
- (iii) Nn = {e}.
7.6.2. Proposition. A finite group G is solvable if and only if there
exists a finite chain of subgroups
G = N0
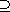 N1 N1
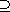 � �
� � �
� 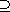 Nn
such that Nn
such that
- (i) Ni is a normal subgroup in Ni-1 for i =
1,2, . . . ,n,
- (ii) Ni-1 / Ni is cyclic of prime order for
i = 1,2, . . . ,n, and
- (iii) Nn = {e}.
7.6.3. Theorem. Let p be a prime number. Any finite p-group is
solvable.
7.6.4. Definition. Let G be a group. An element g
 G is called a
commutator if G is called a
commutator if
g = aba-1b-1
for elements a,b
 G. The
smallest subgroup that contains all commutators of G is called the commutator
subgroup or derived subgroup of G, and is denoted by G'. G. The
smallest subgroup that contains all commutators of G is called the commutator
subgroup or derived subgroup of G, and is denoted by G'.
7.6.5. Proposition. Let G be a group with commutator subgroup G'.
- (a) The subgroup G' is normal in G, and the factor group G/G' is
abelian.
- (b) If N is any normal subgroup of G, then the factor group G/N
is abelian if and only if G'
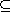 N. N.
7.6.6. Definition. Let G be a group. The subgroup (G' )' is called the
second derived subgroup of G. We define G(k) inductively as (G(k-1))',
and call it the k th derived subgroup
7.6.7. Theorem. A group G is solvable if and only if G(n) =
{e} for some positive integer n.
7.6.8. Corollary. Let G be a group.
- (a) If G is solvable, then so is any subgroup or homomorphic
image of G.
- (b) If N is a normal subgroup of G such that both N and G/N are
solvable, then G is solvable.
7.6.9. Definition. Let G be a group. A chain of subgroups
G = N0
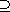 N1 N1
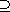 . . . . . .
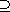 Nn
such that Nn
such that
- (i) Ni is a normal subgroup in Ni-1 for i =
1,2, . . . ,n,
- (ii) Ni-1 / Ni is simple for i = 1,2, . . .
,n, and
- (iii) Nn = {e}
is called a composition series The factor groups Ni-1 / Ni
are called the composition factors determined by the series.
7.6.10. Theorem. [Jordan-Holder] Any two composition series for a
finite group have the same length. Furthermore, there exists a one-to-one
correspondence between composition factors of the two composition series under
which corresponding composition factors are isomorphic.
Simple groups
7.7.1. Lemma. If n
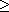 3, then
every permutation in An can be expressed as a product of 3-cycles. 3, then
every permutation in An can be expressed as a product of 3-cycles.
7.7.2. Theorem. The symmetric group Sn is not solvable for
n 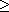 5. 5.
7.7.3. Lemma. If n
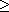 4, then no
proper normal subgroup of An contains a 3-cycle. 4, then no
proper normal subgroup of An contains a 3-cycle.
7.7.4. Theorem. The alternating group An is simple if n
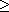 5. 5.
7.7.5. Definition. Let F be a field. The set of all n � n matrices
with entries in F and determinant 1 is called the special linear group
over F, and is denoted by SLn(F).
The group SLn(F) modulo its center is called the projective
special linear group and is denoted by PSLn(F).
7.7.6. Proposition. For any field F, the center of SLn(F)
is the set of nonzero scalar matrices with determinant 1.
Example. 7.7.1. PSL2(F)
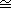 S3
if |F| = 2. S3
if |F| = 2.
Example. 7.7.2. PSL2(F)
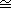 A4
if |F| = 3. A4
if |F| = 3.
7.7.7. Lemma. Let F be any field. Then SL2(F) is generated
by elements of the form
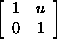 and and
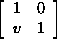 . .
7.7.8. Lemma. Let F be any finite field, and let N be a normal
subgroup of SL2(F). If N contains an element of the form
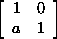 with a with a
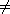 0, then N =
SL2(F). 0, then N =
SL2(F).
7.7.9. Theorem. Let F be any finite field with |F| > 3. Then the
projective special linear group PSL2(F) is a simple group.
|

