Looking for GATE Preparation Material? Join & Get here now!

** Gate 2013 Question Papers.. ** CEED 2013 Results.. ** Gate 2013 Question Papers With Solutions.. ** GATE 2013 CUT-OFFs.. ** GATE 2013 Results.. **

Harmonic functions

Harmonic functions

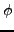
Definition 3.4.1 Let $\phi$ be a function of two real variables

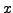
and

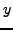
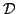
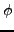
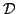
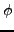
, defined over a domain $\mathcal{D}$ . Suppose that $\phi$ has second order partial derivatives on $\mathcal{D}$ . The function $\phi$ is called an harmonic function if it verifies the equation:

$\displaystyle \phi_{xx}+\phi_{yy}=0$

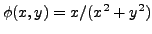
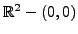
Example 3.4.2 Take $\phi (x,y)= x/(x^2+y^2)$ . Then over $\mathbb{R}^2-{(0,0)}$ we have:

$\displaystyle \phi _x$	$\displaystyle = \frac {y^2-x^2}{(x^2+y^2)^2};$
$\displaystyle \phi _y$	$\displaystyle = \frac {-2xy}{(x^2+y^2)^2};$
$\displaystyle \phi _{xx}$	$\displaystyle = \frac {2x(x^2-3y^2}{(x^2+y^2)^3};$
$\displaystyle \phi _{yy}$	$\displaystyle = \frac {2x}{(3y^2-x^2)^3}.$

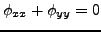
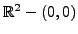
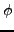
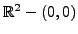
It follows that $\phi_{xx}+\phi_{yy}=0$ over $\mathbb{R}^2-{(0,0)}$ , i.e. $\phi$ is harmonic $\mathbb{R}^2-{(0,0)}$ .

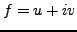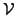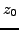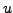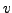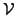Now suppose that is analytic in a neighborhood $\mathcal{V}$ of . Moreover suppose that the partial derivatives of and are differentiable and that the second partial derivatives are continuous functions on $\mathcal{V}$ . From Cauchy-Riemann equations follows:

$\begin{displaymath}\begin{cases}u_{xx}=v_{yx} \ u_{xy}=v_{yy} \end{cases} \qqua... ...\qquad \begin{cases}u_{yx}=-v{xx} \ u_{yy}=-v_{xy} \end{cases}\end{displaymath}$

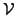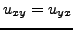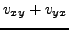As the second partial derivatives are continuous on $\mathcal{V}$ , we have $u_{xy}=u_{yx}$ and $v_{xy}+v_{yx}$ . It follows that:

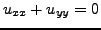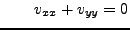$\displaystyle u_{xx}+u_{yy}=0$ and $\displaystyle \qquad v_{xx}+v_{yy}=0$

The computations that we performed before Definition 4.1 can be summarized in a theorem:

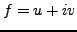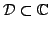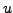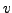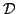Theorem 3.4.3 If is a function of a complex variable, analytic over a domain $\mathcal{D} \subset \mathbb{C}$ , then and are harmonic over $\mathcal{D}$ .

Example 3.4.4 Let

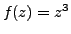
. The function is an entire function, as we proved previously. With

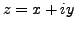
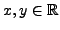
and $x,y \in \mathbb{R}$ , we have:

$\displaystyle f(z)=(x+iy)^3=\underbrace{x^3-3xy^2)}_{=u(x,y)}+i \underbrace{(3x^2y-y^3)}_{=v(x,y)}.$

On the one hand, e have:

$\begin{displaymath}\begin{cases}u_x=3x^2-3y^2 \ u_y= -6xy \end{cases} \Longrigh... ...}=6x \ u_{yy}=-6x \end{cases} \Longrightarrow u_{xx}+u_{yy}=0.\end{displaymath}$

On the other hand, we have:

$\begin{displaymath}\begin{cases}v_x=6xy \ v_y= 3x^2-3y^2 \end{cases} \Longright... ...}=6y \ v_{yy}=-6y \end{cases} \Longrightarrow v_{xx}+v_{yy}=0.\end{displaymath}$

The functions

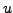
and

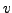
are both harmonic.

Definition 3.4.5 Let

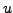
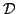
be a function of two real variables, harmonic over a domain $\mathcal{D}$ . Let

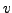
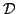
be a function of two real variables, defined over $\mathcal{D}$ , and such that

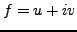
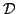
is analytic over $\mathcal{D}$ . Then

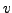
is called an harmonic conjugate of

Example 3.4.6 Let

. This is a polynomial function, thus it has partial derivatives of any order.

(i)

The function

is harmonic:

$\begin{align*}\begin{cases}u_x=2x \ u_y=-2y \end{cases} \Longrightarrow \begin{... ...{xx}=2 \ u_{yy}=-2 \end{cases} \Longrightarrow u_{xx}+u_{yy}=2-2=0.\end{align*}$

(ii)

If there exists

such that

is analytic over $\mathbb{C}$ , then

and

verify the Cauchy-Riemann equations (v.s. section 3):

$\begin{displaymath}\begin{cases}v_x=-u_y \ v_y=u_x \end{cases} \Longrightarrow ... ...\begin{cases}v(x,y)=2xy+C_1(y) \ v(x,y)=2xy+C_2(x) \end{cases}\end{displaymath}$

where

and

are independent of

and

respectively. As these two formulas define the same function,

and

must be constant, i.e.

, where $k \in \mathbb{R}$ .

(iii)

Finally, we have:

$\displaystyle f(z)= x^2-y^2 +i(2xy+k).$

Please compare this with example 2.1.

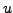
We can now discover another important property of the analytic conjugates.

Theorem 3.4.7 Let 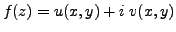$f(z)=u(x,y)+i\; v(x,y)$ , as usual. Suppose that 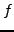is analytic over some domain 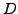. Then the level curves of 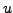are orthogonal to the level curves of .

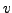Proof. Use Cauchy-Riemann equations and show that the gradients of

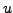
and

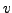
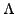
are orthogonal, whence the result. $\qedsymbol$

Example 3.4.8 Take $f(z)=z^2, \; z \in \mathbb{C}$ . With the usual algebraic notation, we have

and

For general , then equation defines an equilateral hyperbola, whose symmetry axes are the coordinate axes (red curves in Figure 2), and the equation defines an equilateral hyperbola whose asymptotes are the coordinates axes (blue curves in Figure 2). For , we have the union of the angle bisectors of the coordinate axes and the union of the coordinate axes respectively.

**Figure 2:** Level curves for two harmonic conjugates
$\begin{figure}\mbox{ \epsfig{file=OrthogonalLevelCurves,height=5cm} }\end{figure}$

Discussion Center

Discuss/
Query
Papers/
Syllabus
Feedback/
Suggestion
Yahoo
Groups
Sirfdosti
Groups
Contact
Us

MEMBERS LOGIN

INTERVIEW EBOOK

Get 9,000+ Interview Questions & Answers in an eBook. Interview Question & Answer Guide

9,000+ Interview Questions
All Questions Answered
5 FREE Bonuses
Free Upgrades

GATE RESOURCES

Gate Books

Training Institutes

Gate FAQs

GATE BOOKS

Mechanical Engineeering Books

Robotics Automations Engineering Books

Civil Engineering Books

Chemical Engineering Books

Environmental Engineering Books

Electrical Engineering Books

Electronics Engineering Books

Information Technology Books

Software Engineering Books

GATE Preparation Books

Exciting Offers

GATE Exam, Gate 2009, Gate Papers, Gate Preparation & Related Pages GATE Overview \| GATE Eligibility \| Structure Of GATE \| GATE Training Institutes \| Colleges Providing M.Tech/M.E. \| GATE Score \| GATE Results \| PG with Scholarships \| Article On GATE \| GATE Forum \| GATE 2009 Exclusive \| GATE 2009 Syllabus \| GATE Organizing Institute \| Important Dates for GATE Exam \| How to Apply for GATE \| Discipline / Branch Codes \| GATE Syllabus for Aerospace Engineering \| GATE Syllabus for Agricultural Engineering \| GATE Syllabus for Architecture and Planning \| GATE Syllabus for Chemical Engineering \| GATE Syllabus for Chemistry \| GATE Syllabus for Civil Engineering \| GATE Syllabus for Computer Science / IT \| GATE Syllabus for Electronics and Communication Engineering \| GATE Syllabus for Engineering Sciences \| GATE Syllabus for Geology and Geophysics \| GATE Syllabus for Instrumentation Engineering \| GATE Syllabus for Life Sciences \| GATE Syllabus for Mathematics \| GATE Syllabus for Mechanical Engineering \| GATE Syllabus for Metallurgical Engineering \| GATE Syllabus for Mining Engineering \| GATE Syllabus for Physics \| GATE Syllabus for Production and Industrial Engineering \| GATE Syllabus for Pharmaceutical Sciences \| GATE Syllabus for Textile Engineering and Fibre Science \| GATE Preparation \| GATE Pattern \| GATE Tips & Tricks \| GATE Compare Evaluation \| GATE Sample Papers \| GATE Downloads \| Experts View on GATE \| CEED 2009 \| CEED 2009 Exam \| Eligibility for CEED Exam \| Application forms of CEED Exam \| Important Dates of CEED Exam \| Contact Address for CEED Exam \| CEED Examination Centres \| CEED Sample Papers \| Discuss GATE \| GATE Forum of OneStopGATE.com \| GATE Exam Cities \| Contact Details for GATE \| Bank Details for GATE \| GATE Miscellaneous Info \| GATE FAQs \| Advertisement on GATE \| Contact Us on OneStopGATE \|
Copyright © 2024. One Stop Gate.com. All rights reserved	Testimonials \|Link To Us \|Sitemap \|Privacy Policy \| Terms and Conditions\|About Us
Our Portals : Academic Tutorials \| Best eBooksworld \| Beyond Stats \| City Details \| Interview Questions \| India Job Forum \| Excellent Mobiles \| Free Bangalore \| Give Me The Code \| Gog Logo \| Free Classifieds \| Jobs Assist \| Interview Questions \| One Stop FAQs \| One Stop GATE \| One Stop GRE \| One Stop IAS \| One Stop MBA \| One Stop SAP \| One Stop Testing \| Web Hosting \| Quick Site Kit \| Sirf Dosti \| Source Codes World \| Tasty Food \| Tech Archive \| Software Testing Interview Questions \| Free Online Exams \| The Galz \| Top Masala \| Vyom \| Vyom eBooks \| Vyom International \| Vyom Links \| Vyoms \| Vyom World C Interview Questions \| C++ Interview Questions \| Send Free SMS \| Placement Papers \| SMS Jokes \| Cool Forwards \| Romantic Shayari