Looking for GATE Preparation Material? Join & Get here now!

** Gate 2013 Question Papers.. ** CEED 2013 Results.. ** Gate 2013 Question Papers With Solutions.. ** GATE 2013 CUT-OFFs.. ** GATE 2013 Results.. **

Systems of linear equations in Three variables.

SYSTEMS OF EQUATIONS in THREE VARIABLES

It is often desirable or even necessary to use more than one variable to model a situation in a field such as business, science, psychology, engineering, education, and sociology, to name a few. When this is the case, we write and solve a system of equations in order to answer questions about the situation.

If a system of linear equations has at least one solution, it is consistent. If the system has no solutions, it is inconsistent. If the system has an infinity number of solutions, it is dependent. Otherwise it is independent.

A linear equation in three variables is an equation equivalent to the equation
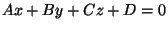
$\displaystyle Ax+By+Cz+D =0$
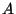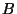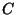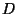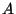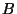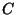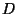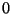where $\displaystyle A$ , $\displaystyle B$ , $\displaystyle C$ , and $\displaystyle D$ are real numbers and $\displaystyle A$ , $\displaystyle B$ , $\displaystyle C$ , and $\displaystyle D$ are not all $\displaystyle 0$ .

Example 1:
John inherited $25,000 and invested part of it in a money market account, part in municipal bonds, and part in a mutual fund. After one year, he received a total of $1,620 in simple interest from the three investments. The money market paid 6% annually, the bonds paid 7% annually, and the mutually fund paid 8% annually. There was $6,000 more invested in the bonds than the mutual funds. Find the amount John invested in each category.

There are three unknowns:
1 : The amount of money invested in the money market account.
2 : The amount of money invested in municipal bonds.
3 : The amount of money invested in a mutual fund.

Let's rewrite the paragraph that asks the question we are to answer.

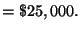
[The amount of money invested in the money market account + [The amount of money invested in municipal bonds ] + [The amount of money invested in a mutual fund ] $\displaystyle =\$25,000.$

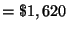
The 6% interest on [ The amount of money invested in the money market account ]+ the 7% interest on [ The amount of money invested in municipal bonds ] + the 8% interest on [ The amount of money invested in a mutual fund ] $\displaystyle =\$1,620$

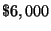[The amount of money invested in municipal bonds ] - [ The amount of money invested in a mutual fund ] = $\displaystyle \$6,000$ .

It is going to get boring if we keep repeating the phrases
1 : The amount of money invested in the money market account.
2 : The amount of money invested in municipal bonds.
3 : The amount of money invested in a mutual fund.

Let's create a shortcut by letting symbols represent these phrases. Let

x = The amount of money invested in the money market account.
y = The amount of money invested in municipal bonds.
z = The amount of money invested in a mutual fund.

in the three sentences, and then rewrite them.

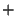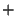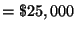The sentence [ The amount of money invested in the money market account ] $\displaystyle +$ [ The amount of money invested in municipal bonds ] $\displaystyle +$ [ The amount of money invested in a mutual fund ] $\displaystyle =\$25,000$ can now be written as
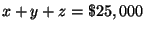
$\displaystyle x+y+z =\$25,000$
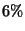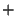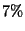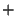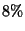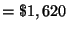The sentence The $\displaystyle 6\%$ interest on [ The amount of money invested in the money market account ] $\displaystyle +$ the $\displaystyle 7\%$ interest on [ The amount of money invested in municipal bonds ] $\displaystyle +$ the $\displaystyle 8\%$ interest on [ The amount of money invested in a mutual fund ] $\displaystyle =\$1,620$ can now be written as
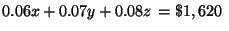
$\displaystyle 0.06x+0.07y+0.08z =\$25,000$
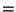
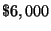The sentence [ The amount of money invested in municipal bonds ] $\displaystyle -$ [ The amount of money invested in a mutual fund ] $\displaystyle =$ $\displaystyle \$6,000$ can now be written as
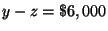
$\displaystyle y-z =\$6,000$

We have converted the problem from one described by words to one that is described by three equations.

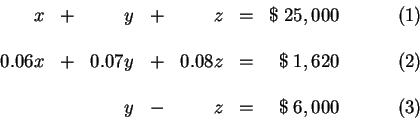
$\begin{displaymath}\begin{array}{rrrrrrrrr} x &+& y &+& z & = & \$ \; 25,000 \\ ... ...\; \begin{array}{r} (1) \\ \\ (2) \\ \\ (3)\\ \end{array}\end{displaymath}$

We are going to show you how to solve this system of equations three different ways:
1)        Substitution,
2)        Elimination,
3)        Matrices.

SUBSTITUTION:
The process of substitution involves several steps:
Step 1:        Solve for one of the variables in one of the equations. It makes no difference which equation and which variable you choose. Let's solve for 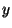$\displaystyle y$ in equation (3) because the equation only has two variables.
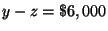
$\displaystyle y-z =\$6,000$
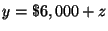
$\displaystyle y =\$6,000+z$
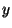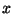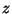Step 2:        Substitute this value for $\displaystyle y$ in equations (1) and (2). This will change equations (1) and (2) to equations in the two variables $\displaystyle x$ and $\displaystyle z$ . Call the changed equations (4) and (5).

$\begin{eqnarray*} x+y+z =\$25,000 \\ x+\left( \$6,000+z\right) +z =\$25,000 \... ... \$6,000+z\right) +0.08z =\$1,620 \\ 0.06x+0.15z =\$1,200 \\ \end{eqnarray*}$

$\begin{displaymath}\begin{array}{rrrrrrrrr} x &+& 2 z & = & \$ \; 19,000 \\ &&&... ...;\;\;\;\;\;\; \begin{array}{r} (4) \\ \\ (5) \\ \end{array}\end{displaymath}$

Step 3: Solve for 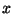$\displaystyle x$ in equation (4).

$\begin{eqnarray*} x+2z =\$19,000 \\ x =\$19,000-2z \\ \end{eqnarray*}$

Step 4: Substitute this value of 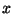$\displaystyle x$ in equation (5). This will give you an equation in one variable.

$\begin{eqnarray*} 0.06x+0.15z =\$1,200 \\ 0.06\left( \$19,000-2z\right) +0.15z =\$1,200 \\ 0.03z =60 \\ \end{eqnarray*}$

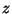Step 5: Solve for $\displaystyle z$ .

$\begin{eqnarray*} 0.03z =60 \\ z =\$2,000 \\ \end{eqnarray*}$

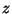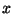Step 6: Substitute this value of $\displaystyle z$ in equation (4) and solve for $\displaystyle x$ .

$\begin{eqnarray*} x+2z =\$19,000 \\ x+2\left( \$2,000\right) =\$19,000 \\ x =\$15,000 \\ \end{eqnarray*}$

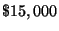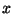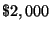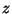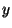Step 7: Substitute $\displaystyle \$15,000$ for $\displaystyle x$ and $\displaystyle \$2,000$ for $\displaystyle z$ in equation (1) and solve for $\displaystyle y$ .

$\begin{eqnarray*} \$15,000+y+\$2,000 =\$25,000 \\ y =\$8,000 \\ \end{eqnarray*}$

The solutions: 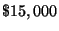$\displaystyle \$15,000$ is invested in the monkey market account, 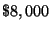$\displaystyle \$8,000$ is invested in the municipal bonds, and 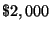$\displaystyle \$2,000$ is invested in mutual funds.
Step 8: Check the solutions:
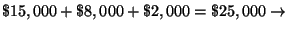$\displaystyle \$15,000+\$8,000+\$2,000 =\$25,000\rightarrow$ Yes
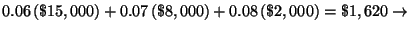$\displaystyle 0.06\left( \$15,000\right) +0.07\left( \$8,000\right) +0.08\left( \$2,000\right) =\$1,620\rightarrow$ Yes
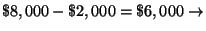$\displaystyle \$8,000-\$2,000 =\$6,000\rightarrow$ Yes

ELIMINATION:
The process of elimination involves several steps: First you reduce three equations to two equations with two variables, and then to one equation with one variable.
Step 1: Decide which variable you will eliminate. It makes no difference which one you choose. Let us eliminate 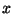$\displaystyle x$ first because 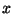$\displaystyle x$ is missing from equation (3).

$\begin{eqnarray*} (1) \: x + y + z = \$25,000 \\ (2) \: 0.06x + 0.07y + 0.08z = \$1,620 \\ (3) \: y - z = \$2,000 \\ \end{eqnarray*}$

Step 2:        Multiply both sides of equation (1) by 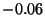$\displaystyle -0.06$ and then add the transformed equation (1) to equation (2) to form equation (4).
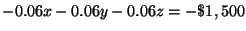
(1) : $\displaystyle -0.06x - 0.06y - 0.06z = -\$1,500$
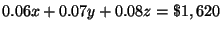
(2) : $\displaystyle 0.06x+0.07y+0.08z =\$1,620$
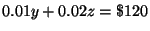
(4) : $\displaystyle 0.01y + 0.02z = \$120$
Step 3:        We now have two equations with two variables.
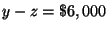
(3) : $\displaystyle y-z=\$2,000$
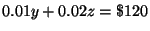
(4) : $\displaystyle 0.01y + 0.02z = \$120$
Step 4:        Multiply both sides of equation (3) by 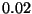$\displaystyle 0.02$ and add to equation (4) to create equation (5) with just one variable.

(3) : $\displaystyle 0.02y - 0.02z = \$120$
(4) : $\displaystyle 0.01y + 0.02z = \$120$
(5) : $\displaystyle 0.03y = \$240$

Step 5:        Solve for 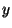$\displaystyle y$ in equation (5).
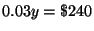
$\displaystyle 0.03y = \$240$
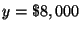
$\displaystyle y =\$8,000$
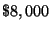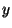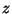Step 6:        Substitute $\displaystyle \$8,000$ for $\displaystyle y$ in equation (3) and solve for $\displaystyle z$ .
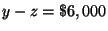
$\displaystyle y-z =\$6,000$
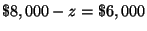
$\displaystyle \$8,000-z =\$6,000$
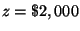
$\displaystyle z =\$2,000$
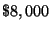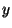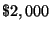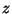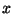Step 7:        Substitute $\displaystyle \$8,000$ for $\displaystyle y$ and $\displaystyle \$2,000$ for $\displaystyle z$ in equation (1) and solve for $\displaystyle x$ .

$\begin{eqnarray*} x+y+z =\$25,000 \\ x+\$8,000+\$2,000 =\$25,000 \\ x =\$15,000 \\ \end{eqnarray*}$

Check your answers as before.

MATRICES:
The process of using matrices is essentially a shortcut of the process of elimination. Each row of the matrix represents an equation and each column represents coefficients of one of the variables.
Step 1: Create a three-row by four-column matrix using coefficients and the constant of each equation.

$\left[ \begin{array}{rrrrrrr} 1 & & 1 & & 1 & \vert & \$25,000 \\ & & & & ... ... & & & & & \vert & \\ 0 & & 1 & & 1 & \vert & \$2,000 \end{array} \right]$

The vertical lines in the matrix stands for the equal signs between both sides of each equation. The first column contains the coefficients of x, the second column contains the coefficients of y, the third column contains the coefficients of z, and the last column contains the constants.
We want to convert the original matrix

$\left[ \begin{array}{rrrrrrr} 1 & & 1 & & 1 & \vert & \$25,000 \\ & & & & ... ... & & & & & \vert & \\ 0 & & 1 & & 1 & \vert & \$2,000 \end{array} \right]$

to the following matrix.

$\left[ \begin{array}{rrrrrrr} 1 & & 0 & & 0 & \vert & a \\ & & & & & \vert... ... b \\ & & & & & \vert & \\ 0 & & 0 & & 1 & \vert & c \end{array} \right]$

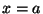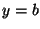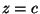Because then you can read the matrix as $\displaystyle x=a$ , $\displaystyle y=b$ , and $\displaystyle z=c$ .
Step 2: We work with column 1 first. The number 1 is already in cell 11(Row1-Col 1). Add 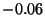$\displaystyle -0.06$ times Row 1 to Row 2 to form a new Row 2.
$\displaystyle -0.06\left[ Row\ 1\right] +\left[ Row\ 2\right] =\left[ New\ Row\ 2\right]$

$\left[ \begin{array}{rrrrrrr} 1 & & 1 & & 1 & \vert & \$25,000 \\ & & & & ... ... & & & & & \vert & \\ 0 & & 1 & & 1 & \vert & \$2,000 \end{array} \right]$

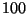Step 3: We will now work with column 1. We want 1 in Cell 22, and we achieve this by multiply Row 2 by $\displaystyle 100$ .
$\displaystyle 100\left[ Row\ 2\right] =\left[ New\ Row\ 2\right]$

$\left[ \begin{array}{rrrrrrr} 1 & & 1 & & 1 & \vert & \$25,000 \\ & & & & ... ... & & & & & \vert & \\ 0 & & 1 & & 1 & \vert & \$2,000 \end{array} \right]$

Step 4: Let's now manipulate the matrix so that there are zeros in Cell 12 and Cell 32. We do this by adding 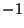$\displaystyle -1$ times Row 2 to Row 1 and Row 3 for a new Row 1 and a new Row 3.

$\begin{eqnarray*} -\left[ Row\ 2\right] +\left[ Row\ 1\right] =\left[ New\ Row\... ...\ 2\right] +\left[ Row\ 3\right] =\left[ New\ Row\ 3\right] \\ \end{eqnarray*}$

$\left[ \begin{array}{rrrrrrr} 1 & & 0 & & -1 & \vert & \$13,000 \\ & & & &... ...& & & & & \vert & \\ 0 & & 0 & & -1 & \vert & -\$2,000 \end{array} \right]$

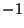Step 5: Let's now manipulate the matrix so that there is a 1 in Cell 33. We do this by multiplying Row 3 by $\displaystyle -1$ .

$\displaystyle -1\left[ Row\ 3\right] =\left[ New\ Row\ 3\right]$

$\left[ \begin{array}{rrrrrrr} 1 & & 0 & & -1 & \vert & \$13,000 \\ & & & &... ... & & & & & \vert & \\ 0 & & 0 & & 1 & \vert & \$2,000 \end{array} \right]$

Step 6: Let's now manipulate the matrix so that there are zeros in Cell 13 and Cell 23. We do this by adding Row 3 to Row 1 for a new Row 1 and adding -2 times Row 3 to Row 3 for a new Row 3.

$\begin{eqnarray*} 1\left[ Row\ 3\right] +\left[ Row\ 1\right] =\left[ New\ Row\... ...w\ 3\right] +\left[ Row\ 2\right] =\left[ New\ Row\ 2\right]\\ \end{eqnarray*}$

$\left[ \begin{array}{rrrrrrr} 1 & & 0 & & 0 & \vert & \$15,000 \\ & & & & ... ... & & & & & \vert & \\ 0 & & 0 & & 1 & \vert & \$2,000 \end{array} \right]$

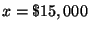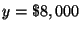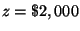You can now read the answers off the matrix: $\displaystyle x=\$15,000$ , $\displaystyle y =\$8,000$ , and $\displaystyle z =\$2,000$ . check your answers by the method described above.

Discussion Center

Discuss/
Query
Papers/
Syllabus
Feedback/
Suggestion
Yahoo
Groups
Sirfdosti
Groups
Contact
Us

MEMBERS LOGIN

INTERVIEW EBOOK

Get 9,000+ Interview Questions & Answers in an eBook. Interview Question & Answer Guide

9,000+ Interview Questions
All Questions Answered
5 FREE Bonuses
Free Upgrades

GATE RESOURCES

Gate Books

Training Institutes

Gate FAQs

GATE BOOKS

Mechanical Engineeering Books

Robotics Automations Engineering Books

Civil Engineering Books

Chemical Engineering Books

Environmental Engineering Books

Electrical Engineering Books

Electronics Engineering Books

Information Technology Books

Software Engineering Books

GATE Preparation Books

Exciting Offers

GATE Exam, Gate 2009, Gate Papers, Gate Preparation & Related Pages GATE Overview \| GATE Eligibility \| Structure Of GATE \| GATE Training Institutes \| Colleges Providing M.Tech/M.E. \| GATE Score \| GATE Results \| PG with Scholarships \| Article On GATE \| GATE Forum \| GATE 2009 Exclusive \| GATE 2009 Syllabus \| GATE Organizing Institute \| Important Dates for GATE Exam \| How to Apply for GATE \| Discipline / Branch Codes \| GATE Syllabus for Aerospace Engineering \| GATE Syllabus for Agricultural Engineering \| GATE Syllabus for Architecture and Planning \| GATE Syllabus for Chemical Engineering \| GATE Syllabus for Chemistry \| GATE Syllabus for Civil Engineering \| GATE Syllabus for Computer Science / IT \| GATE Syllabus for Electronics and Communication Engineering \| GATE Syllabus for Engineering Sciences \| GATE Syllabus for Geology and Geophysics \| GATE Syllabus for Instrumentation Engineering \| GATE Syllabus for Life Sciences \| GATE Syllabus for Mathematics \| GATE Syllabus for Mechanical Engineering \| GATE Syllabus for Metallurgical Engineering \| GATE Syllabus for Mining Engineering \| GATE Syllabus for Physics \| GATE Syllabus for Production and Industrial Engineering \| GATE Syllabus for Pharmaceutical Sciences \| GATE Syllabus for Textile Engineering and Fibre Science \| GATE Preparation \| GATE Pattern \| GATE Tips & Tricks \| GATE Compare Evaluation \| GATE Sample Papers \| GATE Downloads \| Experts View on GATE \| CEED 2009 \| CEED 2009 Exam \| Eligibility for CEED Exam \| Application forms of CEED Exam \| Important Dates of CEED Exam \| Contact Address for CEED Exam \| CEED Examination Centres \| CEED Sample Papers \| Discuss GATE \| GATE Forum of OneStopGATE.com \| GATE Exam Cities \| Contact Details for GATE \| Bank Details for GATE \| GATE Miscellaneous Info \| GATE FAQs \| Advertisement on GATE \| Contact Us on OneStopGATE \|
Copyright © 2024. One Stop Gate.com. All rights reserved	Testimonials \|Link To Us \|Sitemap \|Privacy Policy \| Terms and Conditions\|About Us
Our Portals : Academic Tutorials \| Best eBooksworld \| Beyond Stats \| City Details \| Interview Questions \| India Job Forum \| Excellent Mobiles \| Free Bangalore \| Give Me The Code \| Gog Logo \| Free Classifieds \| Jobs Assist \| Interview Questions \| One Stop FAQs \| One Stop GATE \| One Stop GRE \| One Stop IAS \| One Stop MBA \| One Stop SAP \| One Stop Testing \| Web Hosting \| Quick Site Kit \| Sirf Dosti \| Source Codes World \| Tasty Food \| Tech Archive \| Software Testing Interview Questions \| Free Online Exams \| The Galz \| Top Masala \| Vyom \| Vyom eBooks \| Vyom International \| Vyom Links \| Vyoms \| Vyom World C Interview Questions \| C++ Interview Questions \| Send Free SMS \| Placement Papers \| SMS Jokes \| Cool Forwards \| Romantic Shayari